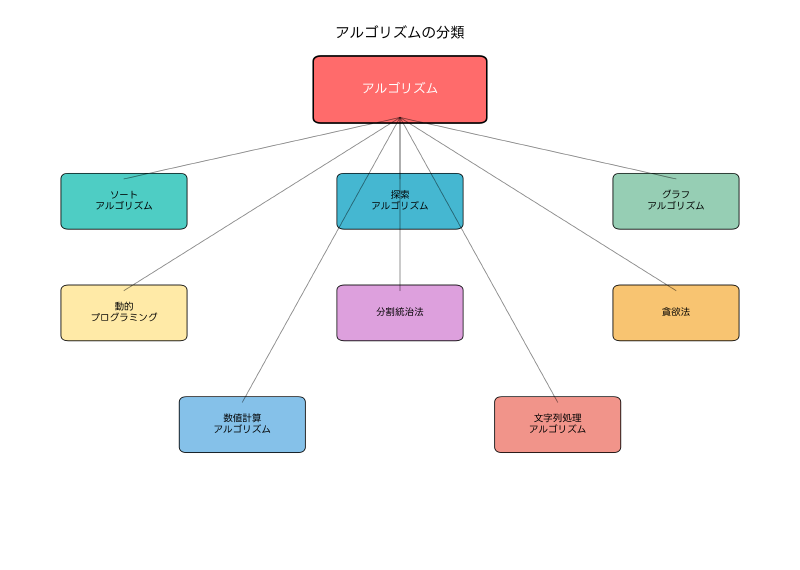
アルゴリズムは、コンピュータサイエンスの根幹を成す重要な概念であり、問題を解決するための明確で効率的な手順を定義したものです。応用情報技術者試験においても、アルゴリズムの理解は必須の知識領域であり、プログラミングからシステム設計まで幅広い分野で活用される基本技術です。現代のソフトウェア開発において、適切なアルゴリズムの選択と実装は、システムの性能と品質を左右する重要な要素となっています。
アルゴリズムとは、特定の問題を解決するために設計された、明確で有限な手順の集合です。良いアルゴリズムは、正確性、効率性、理解しやすさ、汎用性という特徴を持ち、限られた計算資源で最大の効果を発揮します。コンピュータプログラムは、アルゴリズムをプログラミング言語で具体的に実装したものであり、アルゴリズムの品質がプログラムの性能を決定します。
計算量とアルゴリズムの効率性
アルゴリズムの効率性を評価する最も重要な指標が計算量です。計算量には時間計算量と空間計算量があり、それぞれアルゴリズムの実行時間とメモリ使用量を表します。時間計算量は入力サイズに対する実行時間の増加率を示し、Big-O記法を用いて表現されます。
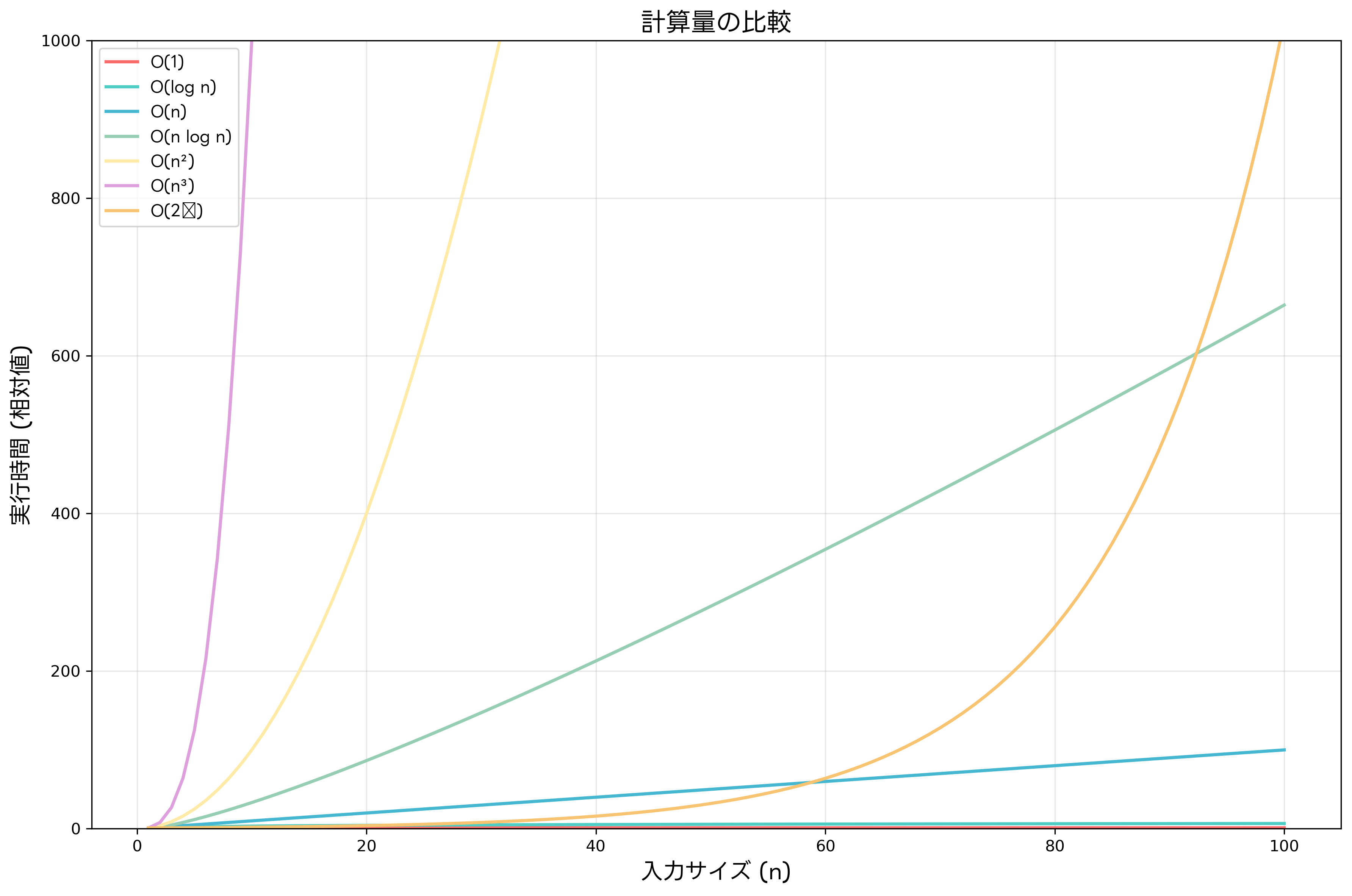
O(1)は定数時間を表し、入力サイズに関係なく一定の時間で処理が完了します。配列の要素への直接アクセスやハッシュテーブルでの検索がこの例です。O(log n)は対数時間を表し、二分探索や平衡二分探索木での操作が該当します。効率的なアルゴリズムを設計する際には、高性能なデータ構造とアルゴリズムの参考書を活用して、理論的背景を深く理解することが重要です。
O(n)は線形時間を表し、配列の全要素を一度ずつ処理する場合に見られます。O(n log n)は準線形時間と呼ばれ、効率的なソートアルゴリズムの多くがこの計算量を持ちます。O(n²)は二次時間を表し、二重ループを使った処理で頻繁に見られます。実際のプログラム開発では、アルゴリズム解析ツールを使用して、コードの計算量を測定し、最適化の方向性を決定することが効果的です。
空間計算量は、アルゴリズムが使用するメモリ量を表します。メモリ効率の良いアルゴリズムは、大量のデータを扱う場合に特に重要であり、組み込みシステムやモバイルアプリケーションでは制約のあるメモリ環境での動作が求められます。現代のプログラミングでは、メモリプロファイリングツールを活用して、メモリ使用量の最適化を図ることが一般的です。
ソートアルゴリズムの世界
ソートアルゴリズムは、データを特定の順序で並び替える手法であり、アルゴリズムの基本的な分類の一つです。データの整理と検索の効率化に不可欠であり、多くのアプリケーションで利用されています。各ソートアルゴリズムには固有の特徴があり、データの性質や制約に応じて最適な手法を選択する必要があります。
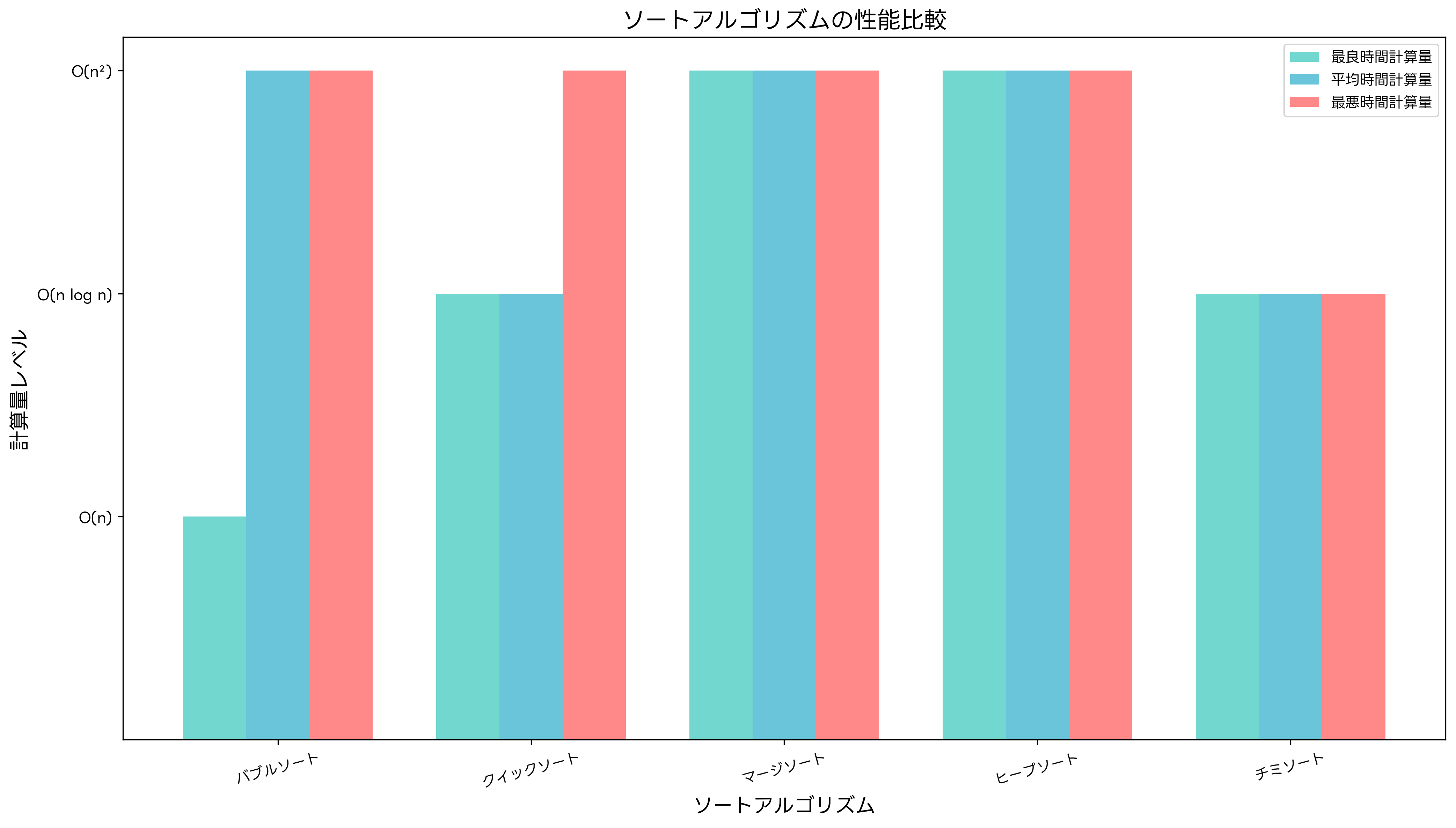
バブルソートは最も単純なソートアルゴリズムの一つですが、時間計算量がO(n²)と非効率的です。隣接する要素を比較して交換を繰り返すため、理解しやすい反面、大量のデータには不向きです。プログラミング学習の初期段階では、アルゴリズム学習用の教材を活用して、基本的なソートアルゴリズムの動作原理を視覚的に理解することが重要です。
クイックソートは分割統治法を用いた効率的なソートアルゴリズムです。平均的な時間計算量はO(n log n)ですが、最悪の場合はO(n²)になることがあります。ピボット要素の選択が性能に大きく影響するため、実装時には注意が必要です。実際の開発現場では、ソートアルゴリズムの実装ライブラリを利用して、高品質な実装を効率的に行うことができます。
マージソートは安定ソートの代表例であり、常にO(n log n)の時間計算量を保証します。分割統治法を用いて配列を再帰的に分割し、マージ処理で結合します。空間計算量はO(n)必要ですが、性能が予測しやすく、大量のデータに適しています。外部ソートにも応用されており、メモリに収まらない大量のデータの処理に使用されます。
ヒープソートは完全二分木の性質を利用したソートアルゴリズムです。最悪の場合でもO(n log n)の時間計算量を保証し、空間計算量はO(1)と効率的です。ヒープデータ構造の理解が必要ですが、メモリ効率の良いソートが実現できます。ヒープ実装の参考書を活用して、ヒープの構築と操作の詳細を学ぶことで、より深い理解が得られます。
探索アルゴリズムの効率性
探索アルゴリズムは、データ集合から特定の要素を見つけ出すための手法です。データの構造と特性に応じて、最適な探索方法を選択することで、検索性能を大幅に向上させることができます。現代の情報システムでは、膨大なデータから必要な情報を迅速に取得することが求められており、効率的な探索アルゴリズムの重要性はますます高まっています。
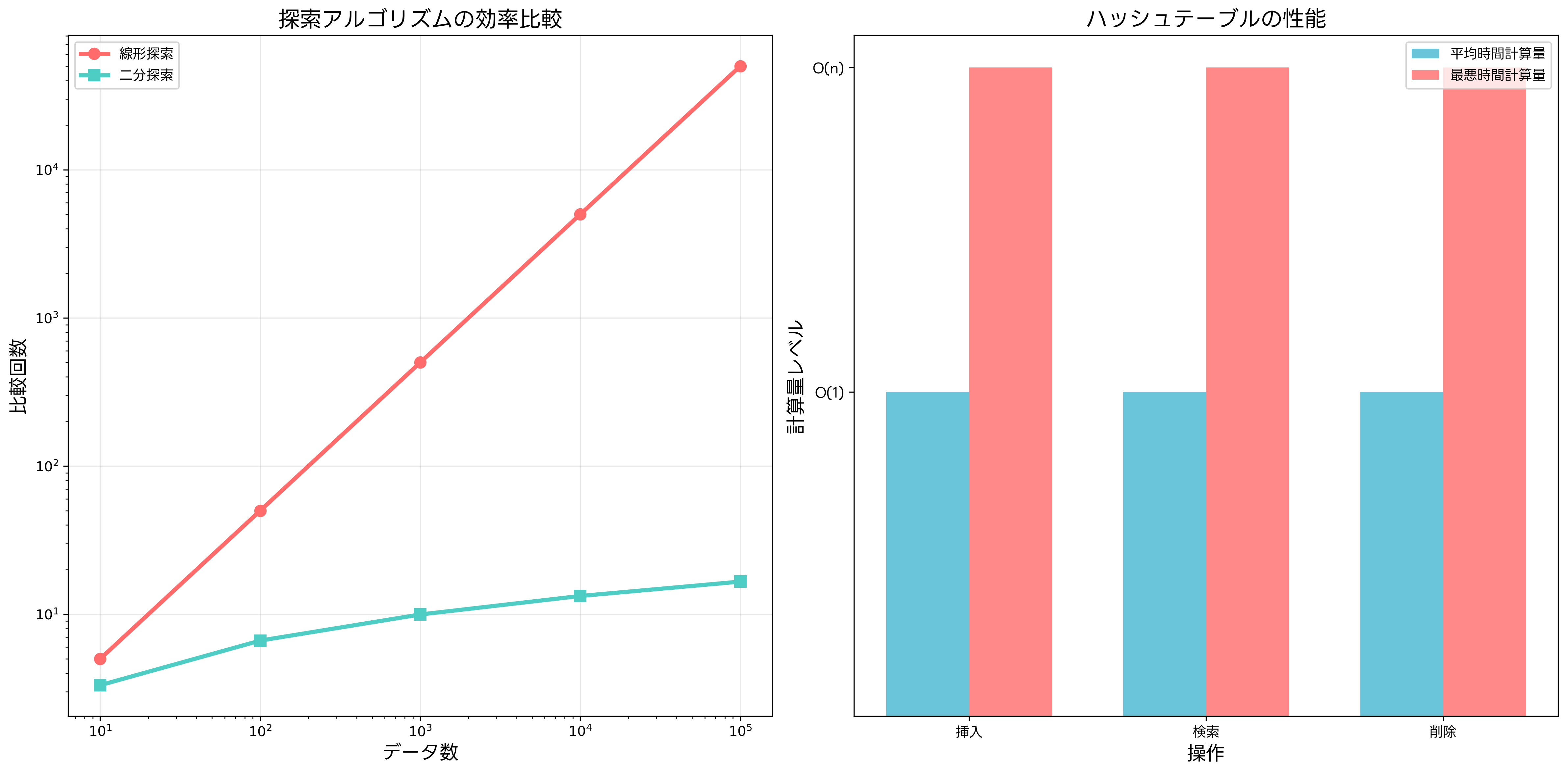
線形探索は最も基本的な探索手法であり、データの先頭から順番に目的の要素を探します。実装が簡単で、データが整列されている必要がありませんが、時間計算量はO(n)となります。小さなデータセットや一回限りの検索には適していますが、大量のデータや頻繁な検索には効率的ではありません。プログラミング初学者には、探索アルゴリズムの入門書を使用して、基本概念から理解を始めることをお勧めします。
二分探索は整列されたデータに対して使用できる効率的な探索手法です。データを半分ずつ除外しながら目的の要素を探すため、時間計算量はO(log n)となります。検索範囲を対数的に減少させることで、大量のデータでも高速な検索が可能です。ただし、データが事前に整列されている必要があり、挿入や削除が頻繁な場合は不向きです。
ハッシュテーブルを用いた探索は、平均的にO(1)の時間計算量で検索を実現できる優秀な手法です。キーをハッシュ関数で変換してインデックスを生成し、直接的にデータにアクセスします。衝突処理の方法によって性能が左右されますが、適切に設計されたハッシュテーブルは非常に高速な検索を提供します。実際のシステム開発では、高性能ハッシュテーブル実装を活用して、効率的なデータ構造を構築できます。
二分探索木は動的な探索構造であり、挿入、削除、検索がすべてO(log n)で実行できます。データの挿入と削除が頻繁な場合に適しており、常に整列された状態を維持します。平衡二分探索木(AVL木、赤黒木など)では、木の高さを一定に保つことで、最悪の場合でもO(log n)の性能を保証します。二分探索木の実装ガイドを参考にして、バランスの取れた木構造の実装技術を習得することが重要です。
動的プログラミングの威力
動的プログラミングは、複雑な問題を小さな部分問題に分割し、それらの解を組み合わせて全体の解を求める手法です。部分問題の解を記録することで、同じ計算の重複を避け、指数時間から多項式時間へと大幅な効率化を実現します。最適化問題や計数問題において特に威力を発揮し、実際のアプリケーションでも幅広く活用されています。
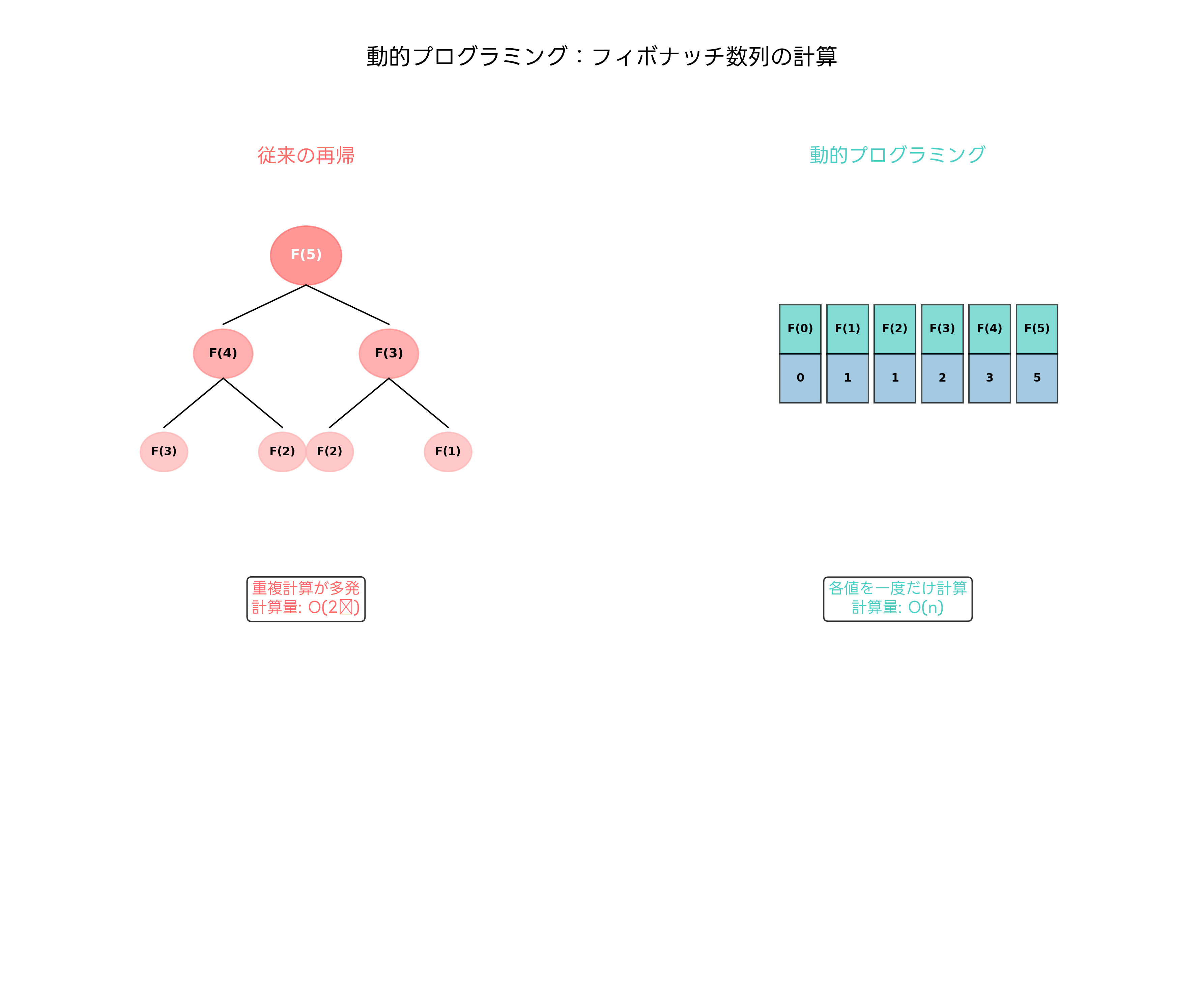
フィボナッチ数列の計算は、動的プログラミングの典型的な例です。naive な再帰実装では同じ部分問題を何度も計算するため、指数時間O(2^n)の計算量となります。しかし、一度計算した結果をテーブルに保存することで、各部分問題を一度だけ計算し、線形時間O(n)で解を求めることができます。この劇的な効率化は、動的プログラミングの本質を示しています。
トップダウン方式(メモ化)では、再帰的に問題を解きながら、計算結果をメモリに保存します。必要な部分問題のみを計算するため、メモリ効率が良く、理解しやすい実装となります。一方、ボトムアップ方式では、小さな部分問題から順次解を構築していきます。反復的な実装となり、関数呼び出しのオーバーヘッドがないため、実行効率が良好です。動的プログラミングの専門書を活用して、両方のアプローチを習得することが重要です。
最長共通部分列問題、ナップサック問題、最短路問題など、多くの最適化問題が動的プログラミングで効率的に解決できます。これらの問題は、実際のシステム開発でも頻繁に遭遇する課題であり、適切なアルゴリズムの選択が性能に直結します。実装時には、アルゴリズム問題集を使用して、様々な問題パターンに対する解法を練習することが効果的です。
状態空間の設計が動的プログラミングの成功の鍵となります。問題を適切な状態で表現し、状態間の遷移関係を明確に定義することで、効率的な解法を構築できます。実際の開発では、動的プログラミング実装ツールを利用して、複雑な状態管理を効率化することも可能です。
グラフアルゴリズムの応用
グラフアルゴリズムは、ネットワーク構造を持つデータを効率的に処理するための手法です。ソーシャルネットワーク、交通網、通信ネットワーク、Webリンク構造など、現実世界の多くの問題をグラフとしてモデル化し、アルゴリズムで解決できます。グラフの表現方法、探索手法、最短路問題、最小全域木問題など、多様なアルゴリズムが存在します。
深さ優先探索(DFS)は、グラフの一つの頂点から開始して、可能な限り深く探索を進める手法です。スタックを使用した実装や再帰的な実装が可能で、連結成分の検出、トポロジカルソート、強連結成分の発見などに活用されます。迷路の解法や木構造の走査にも応用され、バックトラッキングの基礎となる重要な手法です。
幅優先探索(BFS)は、開始頂点から近い順に探索を進める手法です。キューを使用して実装し、最短路の発見、レベル順走査、二部グラフの判定などに使用されます。重みなしグラフにおける最短路問題では、BFSが最適解を保証します。グラフアルゴリズムの実装書を参考にして、効率的な実装技術を習得することが重要です。
ダイクストラ法は、重み付きグラフにおける単一始点最短路問題を解く代表的なアルゴリズムです。優先度付きキューを使用して、常に最短距離の頂点から探索を進めます。負の重みを持たないグラフに適用可能で、GPSナビゲーション、ネットワークルーティング、ゲームのパスファインディングなど、実用的な応用が豊富です。
最小全域木問題では、クラスカル法とプリム法が代表的なアルゴリズムです。クラスカル法は辺を重みの昇順でソートし、サイクルを作らない辺を順次選択します。プリム法は一つの頂点から開始して、木を段階的に拡張していきます。ネットワーク設計、クラスタリング、回路設計などで活用されており、グラフ理論の応用事例集で具体的な活用方法を学ぶことができます。
アルゴリズム設計の手法
アルゴリズム設計には、問題の性質に応じた様々な手法があります。分割統治法、動的プログラミング、貪欲法、バックトラッキング、ブランチアンドバウンドなど、それぞれに適した問題領域があり、効率的な解法を構築するための強力なツールとなります。
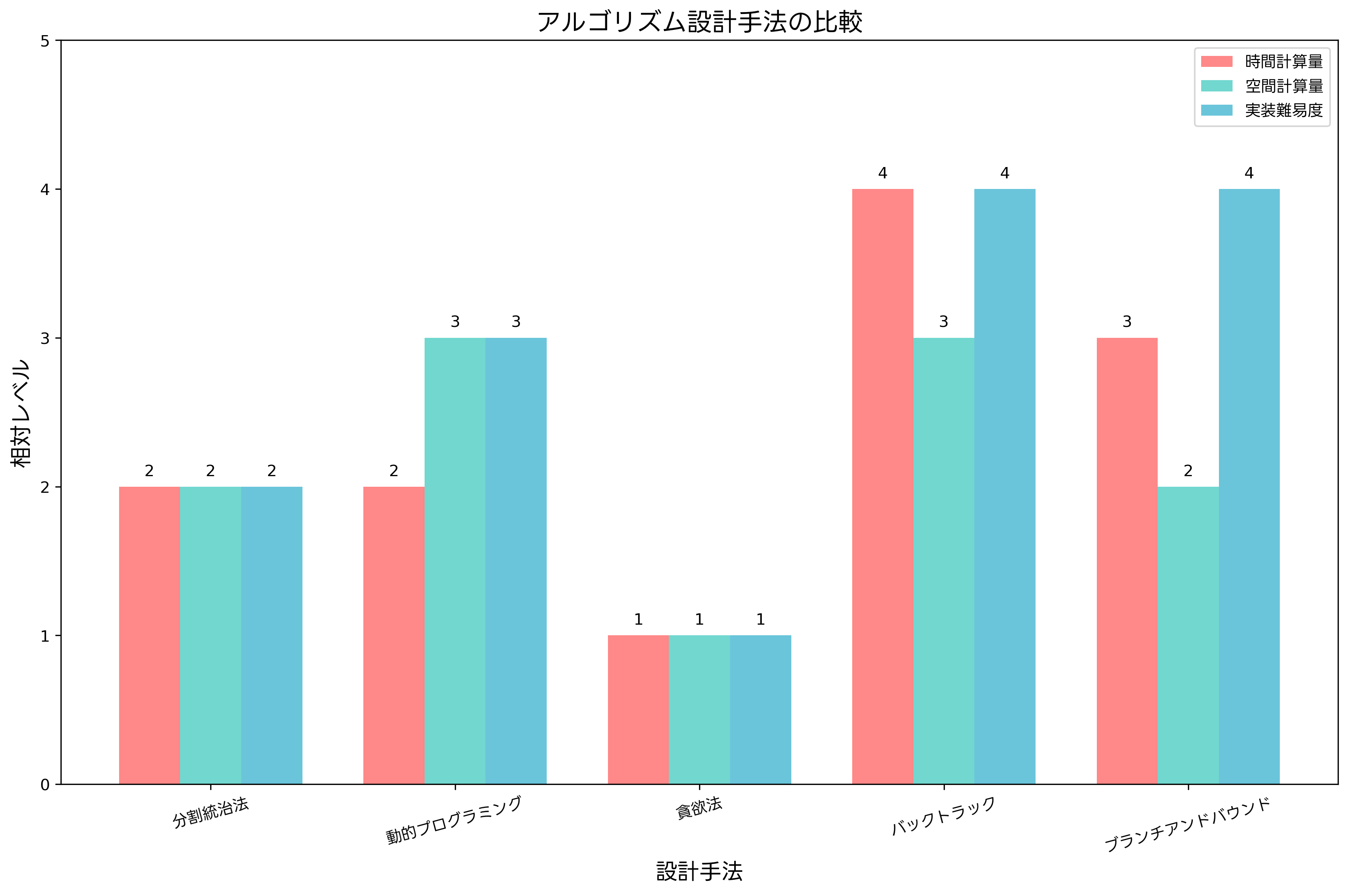
分割統治法は、問題を小さな部分問題に分割し、それぞれを独立に解いてから結果を統合する手法です。クイックソート、マージソート、高速フーリエ変換など、多くの効率的なアルゴリズムがこの手法を採用しています。部分問題が独立であることが重要で、並列処理にも適用しやすい特徴があります。実装時には、分割統治法の設計パターンを参考にして、適切な分割方法を選択することが重要です。
貪欲法は、各段階で局所的に最適な選択を行うことで、全体の解を構築する手法です。実装が簡潔で理解しやすい反面、必ずしも最適解を保証しません。貪欲選択性と最適部分構造を満たす問題に対してのみ最適解を得られます。フラクショナルナップサック問題、最小全域木問題、作業スケジューリング問題などで威力を発揮します。
バックトラッキングは、解空間を系統的に探索し、制約を満たさない部分は早期に除外する手法です。N-Queen問題、数独、グラフ彩色問題などの制約充足問題に適用されます。解空間が指数的に大きい場合でも、効果的な枝刈りにより実用的な時間で解を発見できることがあります。バックトラッキング実装テクニックを学ぶことで、効率的な探索戦略を習得できます。
ブランチアンドバウンド法は、最適化問題において、下界値を利用して探索空間を効率的に削減する手法です。整数線形計画問題、巡回セールスマン問題、ナップサック問題などの組み合わせ最適化問題に適用されます。上界値と下界値を用いた枝刈りにより、指数的な探索空間を大幅に削減できます。
応用情報技術者試験での出題傾向
応用情報技術者試験においては、アルゴリズムに関する問題が午前・午後ともに高い頻度で出題されています。基本的なアルゴリズムの理解から、複雑な問題に対するアルゴリズム設計まで、幅広い知識と応用力が求められます。特に午後問題では、疑似コードやフローチャートを用いた実践的な問題が多く見られます。
午前問題では、ソートアルゴリズムの時間計算量、探索アルゴリズムの特徴、データ構造の操作などの基礎知識が問われます。計算量の比較、アルゴリズムの適用場面、データ構造の選択基準などが頻出テーマです。これらの問題に対応するため、応用情報技術者試験のアルゴリズム対策書を活用して、体系的な知識を身につけることが重要です。
午後問題では、具体的な問題に対するアルゴリズム設計が求められます。疑似コードの空欄補充、フローチャートの完成、計算量の評価などが典型的な出題形式です。動的プログラミング、グラフアルゴリズム、文字列処理などの高度なアルゴリズムも出題されるため、幅広い知識が必要です。
試験対策としては、基本的なアルゴリズムの動作原理を理解し、手作業でのトレースができるレベルまで習得することが重要です。アルゴリズムトレーニング問題集を使用して、様々な問題パターンに慣れ親しむことで、試験での対応力を向上させることができます。
実装経験も重要な要素です。実際にプログラムを書いてアルゴリズムを動作させることで、理論的な理解が深まります。プログラミング演習環境を整備して、継続的な実装練習を行うことで、応用力を身につけることができます。
現代的なアルゴリズムの発展
近年、機械学習、人工知能、ビッグデータ処理などの分野で、新しいアルゴリズムが次々と開発されています。従来のアルゴリズムに加えて、これらの新しい手法を理解することは、現代のソフトウェア開発者にとって重要なスキルとなっています。
機械学習アルゴリズムは、データからパターンを学習し、予測や分類を行う手法です。教師あり学習、教師なし学習、強化学習など、問題の性質に応じて適切な手法を選択します。線形回帰、決定木、ニューラルネットワーク、サポートベクトルマシンなど、多様なアルゴリズムが存在します。機械学習アルゴリズムの実装ガイドを活用して、実際の問題への適用方法を学ぶことができます。
並列アルゴリズムは、マルチコアプロセッサーやクラスターシステムの性能を最大限に活用するための手法です。タスクの分割、負荷分散、同期処理などの技術により、計算時間の大幅な短縮を実現します。MapReduce、分散ソート、並列グラフアルゴリズムなどが代表例です。
近似アルゴリズムは、厳密解の計算が困難な問題に対して、高品質な近似解を効率的に求める手法です。組み合わせ最適化問題において、実用的な時間で許容可能な解を得るために重要です。巡回セールスマン問題、集合カバー問題、最大カット問題などで活用されています。近似アルゴリズムの理論と実践を参考にして、現実的な問題解決手法を習得することができます。
オンラインアルゴリズムは、入力データが逐次的に与えられる環境で動作するアルゴリズムです。キャッシング、負荷分散、ストリーミングデータ処理などで重要な役割を果たします。競合比を用いた性能評価により、最悪ケースでの性能保証を提供します。
実装とデバッグのベストプラクティス
アルゴリズムの実装においては、正確性と効率性の両方を確保することが重要です。コードの可読性を保ちながら、最適化された実装を行うためには、体系的なアプローチが必要です。テストケースの設計、境界値の処理、エラーハンドリングなど、実装の各段階で注意すべきポイントがあります。
実装の初期段階では、アルゴリズムの動作を明確に理解し、疑似コードやフローチャートで設計を行います。複雑なアルゴリズムは段階的に実装し、各段階でテストを実行して正確性を確認します。アルゴリズム実装のベストプラクティスを参考にして、効率的な開発プロセスを確立することが重要です。
デバッグ手法では、トレース実行、アサーション、単体テストなどを活用します。特に再帰アルゴリズムや動的プログラミングでは、中間状態の確認が重要です。デバッグツールと技法を習得することで、効率的な問題解決が可能になります。
性能測定とプロファイリングにより、実装したアルゴリズムの実際の性能を評価します。理論的な計算量と実測値の比較、ボトルネックの特定、最適化ポイントの発見などを行います。大量のデータでのテストにより、スケーラビリティを確認することも重要です。
まとめ
アルゴリズムは、効率的な問題解決の設計図として、コンピュータサイエンスの中核を成す重要な概念です。基本的なソートや探索から、高度な動的プログラミングやグラフアルゴリズムまで、多様な手法を理解し適切に活用することで、高品質なソフトウェアを開発できます。応用情報技術者試験においても重要な分野であり、理論的な理解と実践的な応用力の両方が求められます。
現代のソフトウェア開発では、アルゴリズムの知識は基盤技術として不可欠です。新しい技術分野の発展とともに、従来のアルゴリズムに加えて機械学習や並列処理などの新しい手法も重要になっています。継続的な学習と実践により、変化する技術環境に対応できる能力を身につけることが重要です。
効率的なアルゴリズムの選択と実装により、システムの性能向上、開発効率の改善、保守性の向上を実現できます。理論と実践のバランスを保ちながら、実際の問題に適用できる実践的なスキルを習得することで、プロフェッショナルなソフトウェア開発者として成長することができます。