クラスタリング：データマイニングの基礎技術と実践的応用

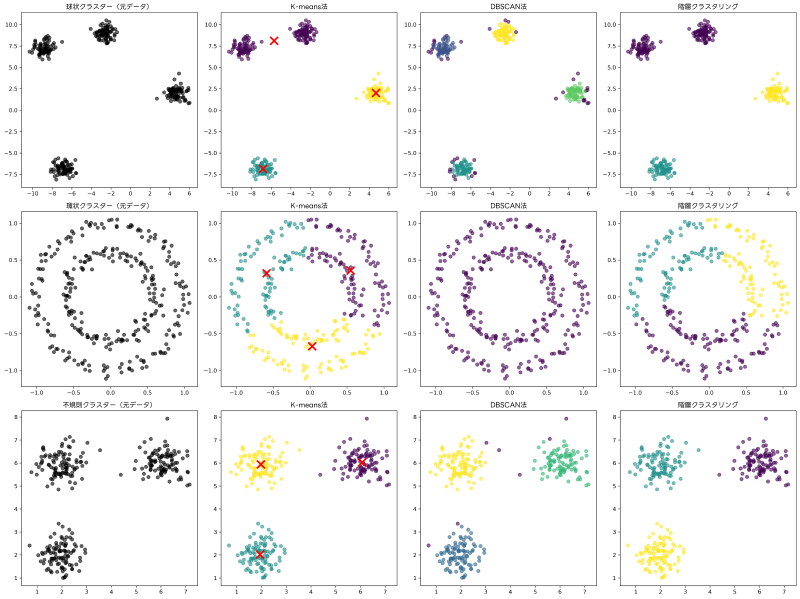
データマイニングと機械学習の分野において、クラスタリングは最も重要で広く活用されている技術の一つです。クラスタリングとは、データ内の類似したオブジェクトを自動的にグループ化する教師なし学習手法であり、データの内在的な構造やパターンを発見するための強力なツールです。応用情報技術者試験においても頻出の重要トピックであり、現代のビッグデータ時代において欠かせない知識となっています。

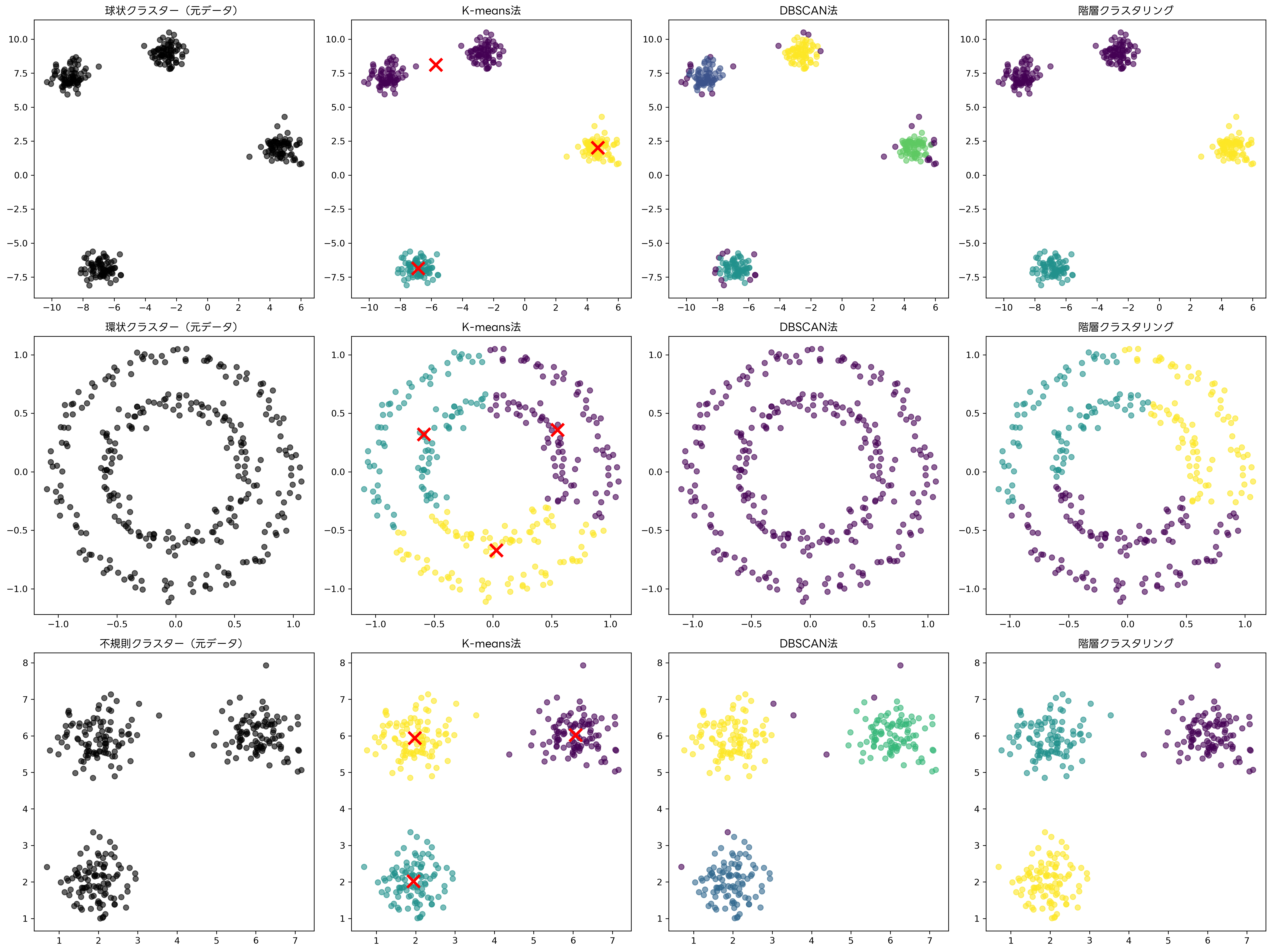
クラスタリング手法の比較

クラスタリング技術は、顧客セグメンテーション、市場分析、画像認識、遺伝子解析、ソーシャルネットワーク分析など、幅広い分野で活用されています。データの量が爆発的に増加している現代において、その膨大なデータから有用な知見を抽出するためのクラスタリング技術の重要性はますます高まっています。

クラスタリングの基本概念と目的

クラスタリングの基本的な目的は、与えられたデータセット内の各データポイントを、類似度の高いもの同士でグループに分割することです。この際、同じクラスター内のデータポイントは互いに類似しており、異なるクラスター間のデータポイントは大きく異なるという特性を持ちます。この特性を定量的に評価するために、距離尺度や類似度指標が用いられます。

一般的に使用される距離尺度には、ユークリッド距離、マンハッタン距離、ミンコフスキー距離、コサイン類似度などがあります。これらの尺度の選択は、データの性質や問題の特性によって決定されます。例えば、数値データにはユークリッド距離、テキストデータにはコサイン類似度が適していることが多いです。

クラスタリング分析を効果的に実施するためには、適切なデータ分析ツールや統計解析ソフトウェアの活用が重要です。また、大規模なデータセットを扱う場合には、高性能コンピューティングシステムの導入により、処理速度の向上が期待できます。

クラスタリングには、階層的手法と非階層的手法の大きく二つのカテゴリーがあります。階層的手法は、データポイント間の階層構造を明示的に表現し、樹形図（デンドログラム）として可視化できる利点があります。一方、非階層的手法は、事前にクラスター数を指定して効率的にクラスタリングを実行できる特徴があります。

K-means法：最も基本的なクラスタリング手法

K-means法は、最も広く知られ、実用的に使用されているクラスタリング手法の一つです。この手法は、事前に指定されたクラスター数kに対して、各クラスターの重心を最適化することで、クラスター内分散を最小化します。アルゴリズムは反復的な最適化プロセスであり、収束するまで重心の更新とデータポイントの再割り当てを繰り返します。

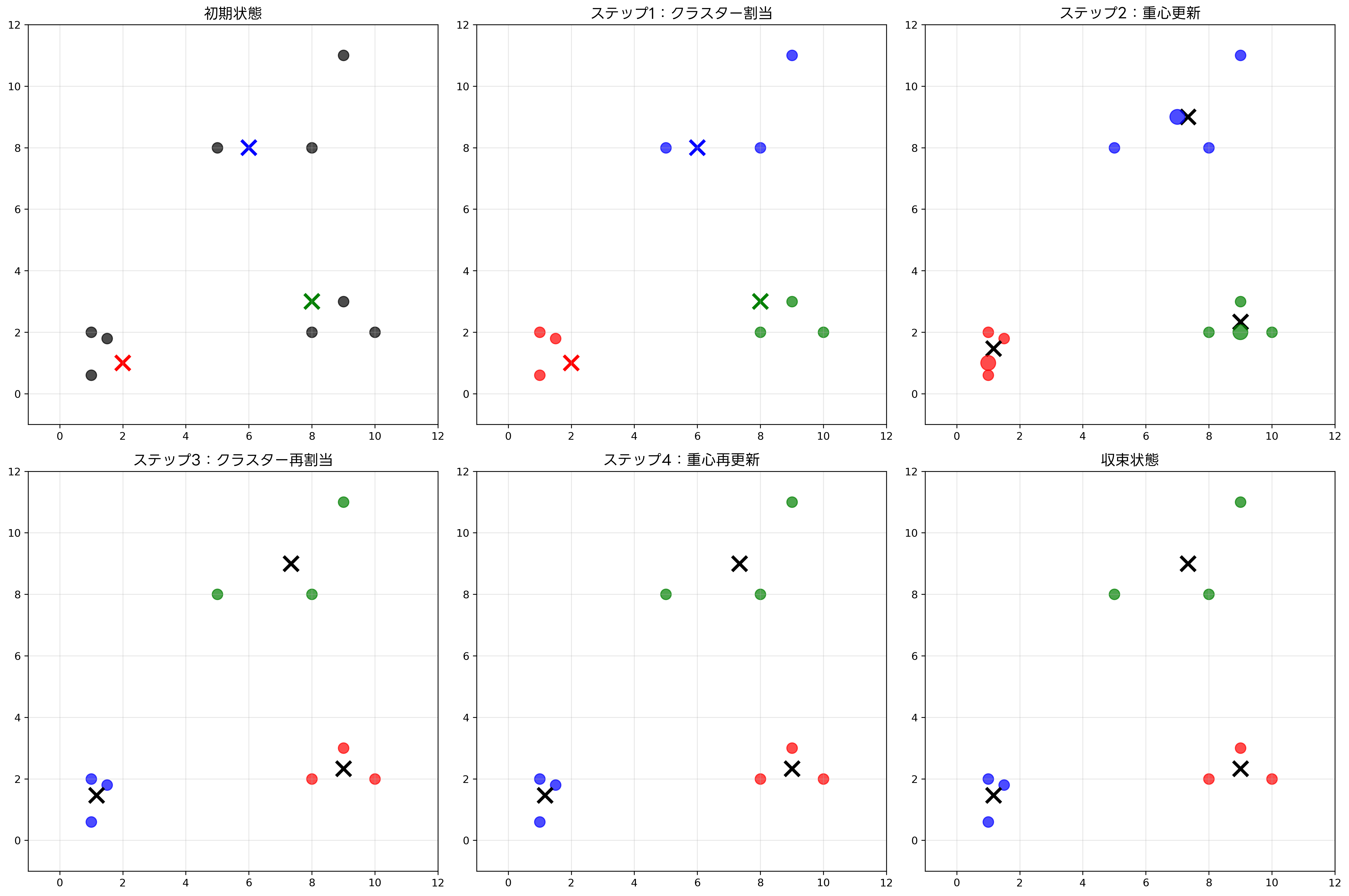
K-means法のアルゴリズム過程

K-means法のアルゴリズムは以下の手順で実行されます。まず、k個の初期重心をランダムに配置します。次に、各データポイントを最も近い重心を持つクラスターに割り当てます。その後、各クラスター内のデータポイントの平均を計算し、新しい重心を決定します。重心が収束するか、最大反復回数に達するまで、このプロセスを繰り返します。

K-means法の実装には、Python機械学習ライブラリやR統計プログラミング環境などのツールが広く利用されています。これらのツールを学習するための機械学習プログラミング書籍も豊富に出版されており、実践的なスキルの習得に役立ちます。

K-means法の主な利点は、アルゴリズムが単純で理解しやすく、大規模なデータセットに対しても比較的高速に動作することです。計算量がO(nkt)（nはデータポイント数、kはクラスター数、tは反復回数）と線形に近いため、ビッグデータの処理にも適用可能です。

しかし、K-means法にはいくつかの制約も存在します。クラスター数kを事前に指定する必要があり、適切なk値の選択は難しい問題です。また、球状でない複雑な形状のクラスターや、密度の異なるクラスターに対しては最適な結果を得られない場合があります。これらの制約を理解し、適切な前処理や他手法との組み合わせを検討することが重要です。

階層クラスタリング：樹形構造でデータ関係を可視化

階層クラスタリングは、データポイント間の階層的な関係を明示的に表現するクラスタリング手法です。この手法は、凝集型（ボトムアップ）と分割型（トップダウン）の二種類に分類されますが、一般的には凝集型階層クラスタリングがよく使用されます。

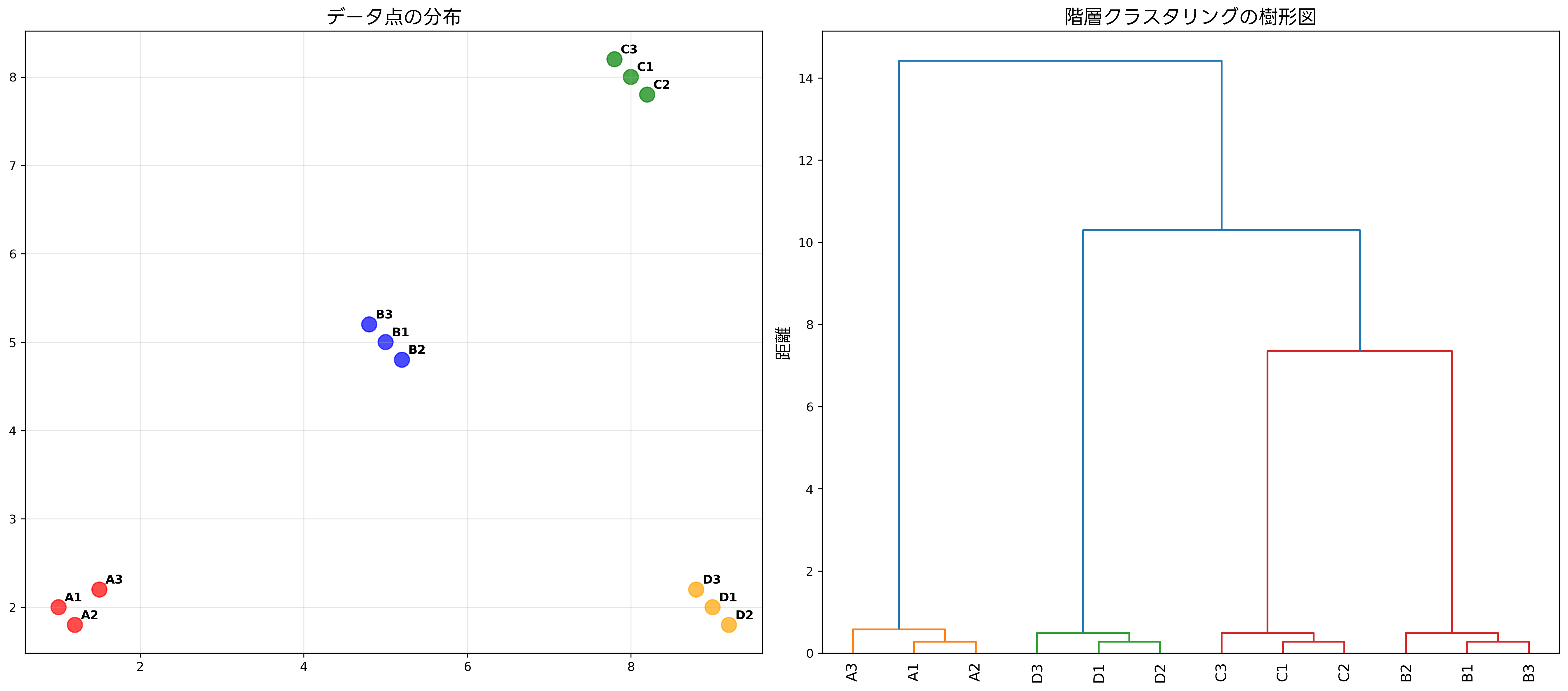
階層クラスタリングの樹形図

凝集型階層クラスタリングのアルゴリズムは、まず各データポイントを個別のクラスターとして初期化します。次に、最も類似した二つのクラスターを見つけて結合し、新しいクラスターを形成します。このプロセスを、すべてのデータポイントが単一のクラスターに統合されるまで繰り返します。

クラスター間の距離の計算には、単連結法、完全連結法、平均連結法、Ward法などの手法が用いられます。単連結法では最も近いポイント間の距離を、完全連結法では最も遠いポイント間の距離を、平均連結法では全ポイント間距離の平均を使用します。Ward法は、クラスター内分散の増加量を最小化する基準でクラスターを結合します。

階層クラスタリングの結果は、デンドログラム（樹形図）として可視化されます。デンドログラムは、クラスターの結合過程と各段階での類似度を視覚的に表現し、適切なクラスター数の決定や、データの階層構造の理解に役立ちます。デンドログラム可視化ツールを使用することで、より詳細で美しい樹形図の作成が可能になります。

階層クラスタリングの利点は、クラスター数を事前に指定する必要がなく、デンドログラムにより結果の解釈が容易であることです。また、決定論的なアルゴリズムであるため、同じデータに対して常に同じ結果が得られます。

しかし、計算量がO(n³)と高次であるため、大規模なデータセットに対しては処理時間が長くなる問題があります。この問題を解決するために、高性能並列計算システムの活用や、効率的なアルゴリズム実装が重要になります。

DBSCAN法：密度ベースのクラスタリング

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）は、密度ベースのクラスタリング手法であり、任意の形状のクラスターを発見し、ノイズポイントを自動的に検出する能力を持ちます。この手法は、K-means法や階層クラスタリングでは困難な、複雑な形状のクラスターに対して優れた性能を発揮します。

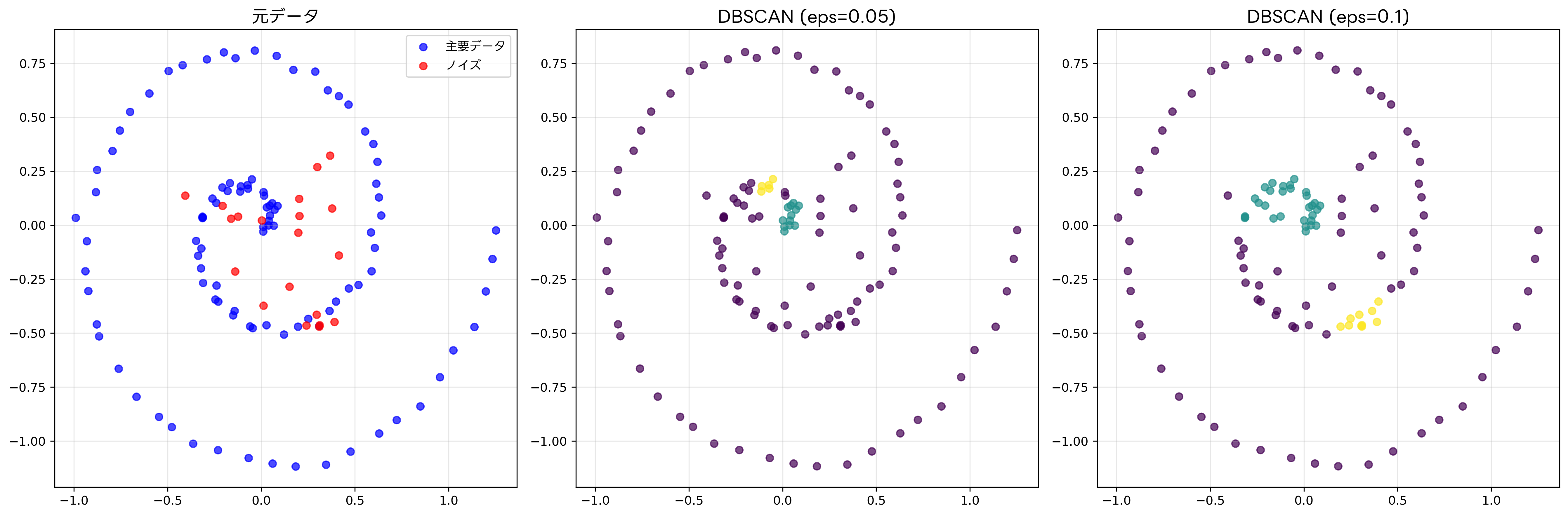
DBSCAN法の密度ベースクラスタリング

DBSCANアルゴリズムは、二つの主要なパラメータを使用します。εは近傍半径を示し、minPtsは密度を判定するための最小ポイント数を表します。アルゴリズムは、各データポイントを核点、境界点、ノイズ点の三つのカテゴリーに分類します。核点は、ε近傍内にminPts以上のポイントを持つポイントです。境界点は核点ではないが核点のε近傍内にあるポイント、ノイズ点はどの核点のε近傍内にもないポイントです。

DBSCANの実行過程では、まず未訪問の核点を見つけて新しいクラスターを開始し、密度接続されたすべてのポイントを同じクラスターに追加します。この過程を、すべてのポイントが訪問されるまで繰り返します。最終的に、どのクラスターにも属さないポイントがノイズとして識別されます。

DBSCANの主な利点は、クラスター数を事前に指定する必要がなく、任意の形状のクラスターを発見でき、ノイズの検出が可能であることです。また、密度の異なる複数のクラスターが混在するデータセットに対しても良好な結果を得られます。

異常検知システムやノイズ除去ツールでは、DBSCANの特性を活用したソリューションが多く開発されています。特に、地理情報システムや画像解析ソフトウェアでは、複雑な空間パターンの検出にDBSCANが活用されています。

ただし、DBSCANはパラメータεとminPtsの設定に敏感であり、適切な値の選択が結果に大きく影響します。また、密度が大きく異なるクラスターが混在する場合には、単一のεでは最適な結果を得られない可能性があります。

ガウス混合モデル：確率的アプローチによるクラスタリング

ガウス混合モデル（Gaussian Mixture Model, GMM）は、データが複数のガウス分布の線形結合によって生成されると仮定する確率的クラスタリング手法です。この手法は、各データポイントが各クラスターに属する確率を提供するため、ソフトクラスタリングとも呼ばれます。

GMMは、EMアルゴリズム（Expectation-Maximization）を使用してパラメータを推定します。Eステップでは、現在のパラメータを用いて各データポイントが各クラスターに属する確率（責任度）を計算します。Mステップでは、計算された責任度を用いて、各ガウス分布のパラメータ（平均、共分散行列、重み）を更新します。

GMMの利点は、楕円形のクラスターを扱うことができ、各データポイントの所属確率を提供することです。これにより、境界領域にあるデータポイントの不確実性を定量的に評価できます。また、AIC（赤池情報量基準）やBIC（ベイズ情報量基準）を使用して、適切なクラスター数を自動選択することも可能です。

確率統計ソフトウェアやベイズ統計ツールでは、GMMを用いた高度な分析機能が提供されています。また、不確実性定量化システムでは、GMMの確率的特性を活用したリスク評価が実施されています。

しかし、GMMは計算量が高く、初期化に敏感で局所解に陥りやすいという問題があります。また、高次元データに対してはパラメータ数が急激に増加し、推定が困難になる場合があります。

クラスタリング結果の評価と検証

クラスタリングは教師なし学習であるため、結果の評価は正解ラベルが存在しない状況で行う必要があります。内部評価指標と外部評価指標の二つのカテゴリーに分けて評価手法を理解することが重要です。

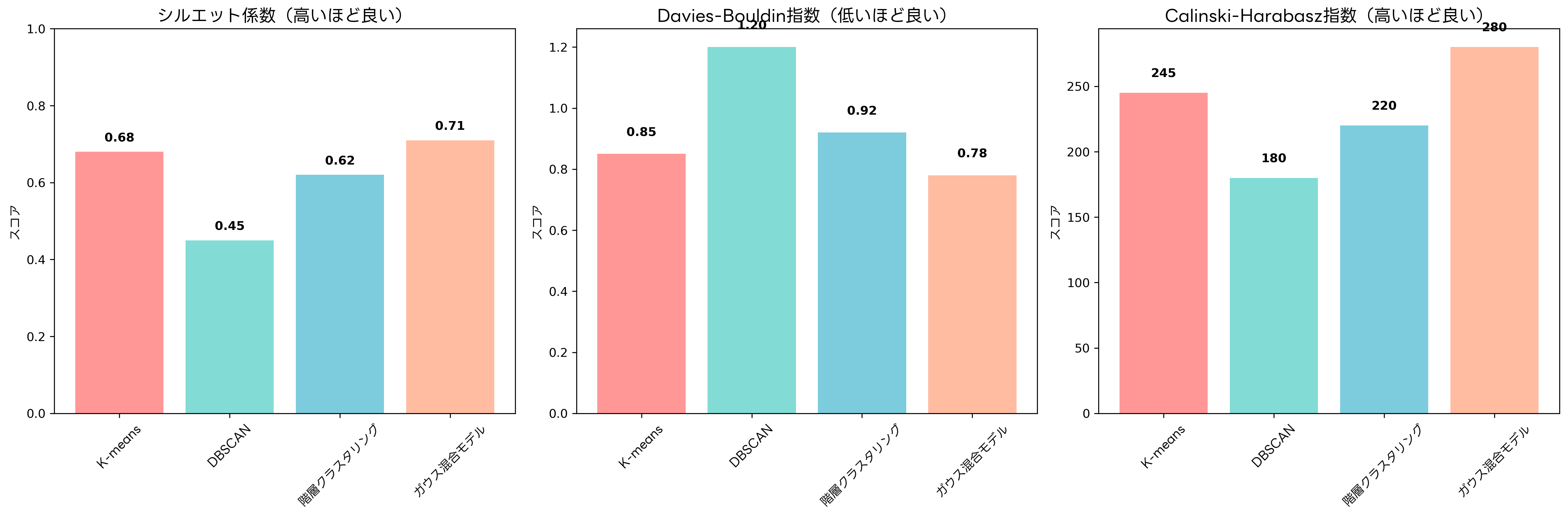
クラスタリング評価指標

内部評価指標は、クラスタリング結果のみを使用して品質を評価する指標です。シルエット係数は最もよく使用される指標の一つで、各データポイントについて、同一クラスター内の他のポイントとの平均距離と、最も近い他クラスターのポイントとの平均距離を比較します。値は-1から1の範囲を取り、1に近いほど良好なクラスタリングを示します。

Davies-Bouldin指数は、クラスター内分散とクラスター間距離の比を評価する指標で、値が小さいほど良好なクラスタリングを表します。Calinski-Harabasz指数は、クラスター間分散とクラスター内分散の比を評価し、値が大きいほど良好な結果を示します。

外部評価指標は、正解ラベルが利用可能な場合に使用される指標です。調整ランド指数（Adjusted Rand Index）、正規化相互情報量（Normalized Mutual Information）、V-measure などがあり、これらは正解との一致度を定量的に評価します。

クラスタリング評価ツールを使用することで、複数の評価指標を同時に計算し、包括的な品質評価が可能になります。また、統計的検定ソフトウェアにより、クラスタリング結果の統計的有意性を検証することもできます。

クロスバリデーションや安定性解析による結果の検証も重要です。データのサブセットや異なるパラメータ設定でクラスタリングを実行し、結果の一貫性を確認することで、信頼性の高いクラスタリングを実現できます。

手法選択の指針と実践的考慮事項

適切なクラスタリング手法の選択は、データの特性、問題の要件、計算資源の制約などを総合的に考慮して行う必要があります。各手法の特徴と適用場面を理解し、実践的な判断基準を持つことが重要です。

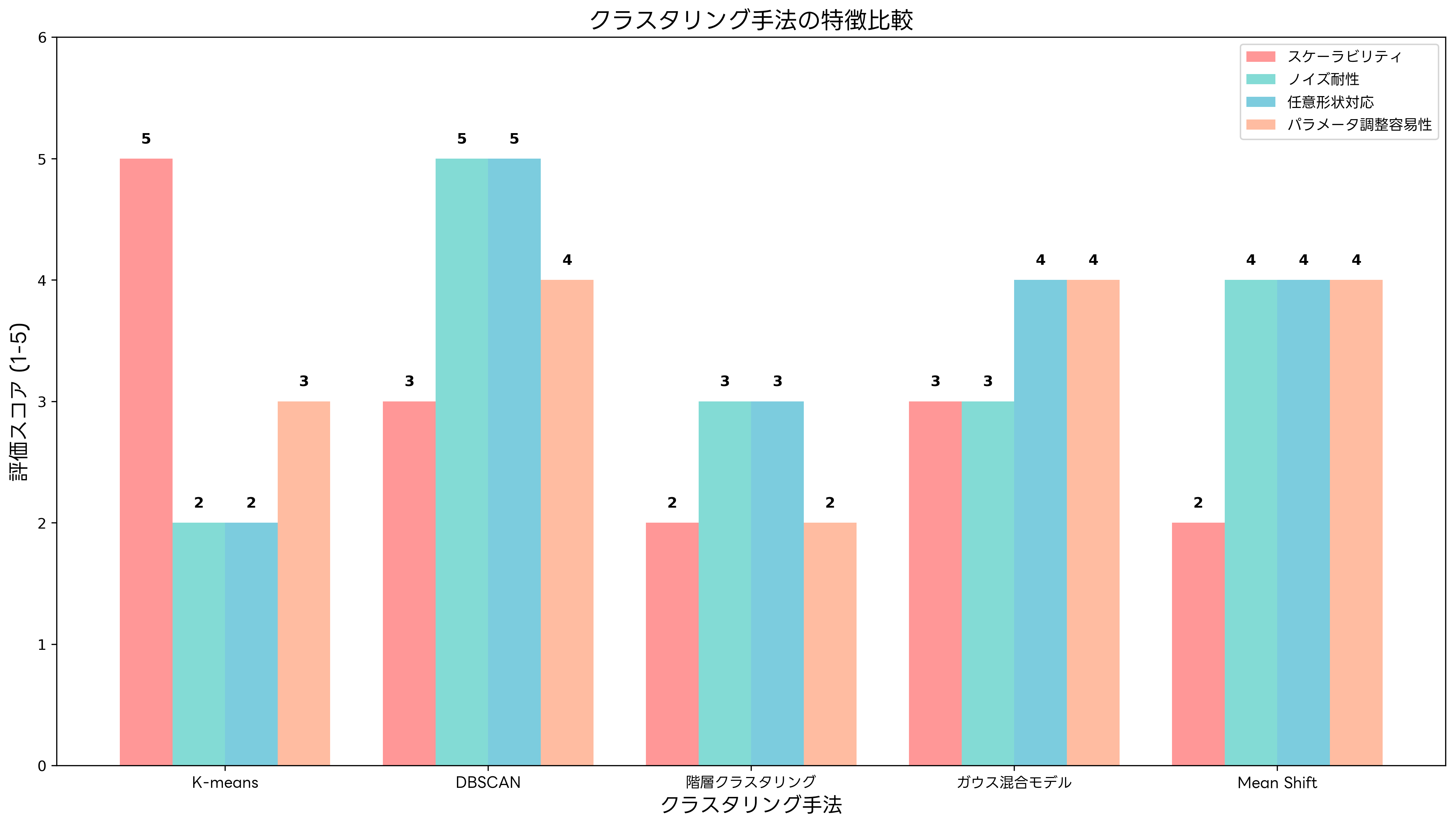
クラスタリング手法の特徴比較

データサイズが小さく（数千ポイント以下）、階層構造の理解が重要な場合には階層クラスタリングが適しています。中規模から大規模なデータセット（数万から数百万ポイント）で、球状のクラスターが想定される場合にはK-means法が効果的です。任意の形状のクラスターが存在し、ノイズの検出が重要な場合にはDBSCANが適しています。

確率的な所属度が必要で、楕円形のクラスターが想定される場合にはガウス混合モデルが有効です。非常に大規模なデータセット（数百万から数億ポイント）に対しては、近似アルゴリズムやオンライン学習手法の検討が必要になります。

ビッグデータ分析プラットフォームや分散コンピューティングシステムの導入により、大規模データに対するクラスタリングの実現が可能になります。また、GPU計算システムを活用することで、並列処理による高速化も期待できます。

実装面では、データの前処理が結果に大きく影響します。正規化やスケーリング、外れ値の除去、次元削減などの前処理を適切に実施することで、クラスタリングの品質を向上させることができます。データ前処理ツールの活用により、効率的な前処理パイプラインの構築が可能です。

パラメータチューニングも重要な要素です。K-means法のクラスター数k、DBSCANのεとminPts、階層クラスタリングの結合基準など、各手法固有のパラメータを適切に設定する必要があります。グリッドサーチやベイズ最適化などのハイパーパラメータ最適化ツールを使用することで、効率的なパラメータ探索が可能になります。

実世界での応用事例と成功要因

クラスタリング技術は、様々な業界や分野で実践的に活用されています。マーケティング分野では、顧客セグメンテーションにより、購買行動や嗜好が類似した顧客グループを特定し、ターゲット広告や商品推薦の精度向上を実現しています。大手小売企業では、数百万人の顧客データをクラスタリングすることで、効果的なマーケティング戦略を策定しています。

顧客分析ソフトウェアやマーケティング自動化システムでは、クラスタリング機能が標準的に搭載されており、ビジネスユーザーでも容易に顧客セグメンテーションを実施できます。

製造業では、品質管理や異常検知にクラスタリングが活用されています。製品の品質データや製造プロセスのセンサーデータをクラスタリングすることで、正常な製品群と異常な製品群を自動識別し、品質向上と不良品削減を実現しています。

バイオインフォマティクス分野では、遺伝子発現データのクラスタリングにより、機能的に類似した遺伝子グループの特定や、病気の亜型分類が行われています。これらの研究には、バイオインフォマティクス解析ツールや遺伝子解析ソフトウェアが広く使用されています。

画像処理や計算機ビジョンの分野では、画像セグメンテーションや物体認識にクラスタリングが応用されています。ピクセルの色情報や特徴量をクラスタリングすることで、画像内の領域分割や物体の抽出を実現します。画像処理ソフトウェアやコンピュータビジョンライブラリでは、高度なクラスタリング機能が提供されています。

応用情報技術者試験での出題傾向と対策

応用情報技術者試験においては、クラスタリングに関する問題が午前問題、午後問題の両方で出題されています。特に、データベースやシステム開発の文脈で、データマイニング技術の一環としてクラスタリングの知識が問われることが多くあります。

午前問題では、クラスタリングの基本概念、主要なアルゴリズムの特徴、評価指標の理解などが問われます。K-means法の収束条件、階層クラスタリングの結合基準、DBSCANのパラメータの意味などが典型的な出題内容です。また、クラスタリングと他の機械学習手法との違いや、適用場面の判断も重要な出題ポイントです。

午後問題では、より実践的な場面でのクラスタリングの応用が問われます。与えられたビジネス課題に対して適切なクラスタリング手法を選択し、期待される結果や注意点を述べる問題や、クラスタリング結果の解釈と活用方法を考察する問題が出題されています。

試験対策としては、応用情報技術者試験対策書で理論的な基礎を固めた上で、データマイニング専門書で実践的な知識を深めることが効果的です。また、過去問題解説集を活用して、出題パターンと解法のポイントを理解することが重要です。

実際にクラスタリングを体験することも有効な学習方法です。プログラミング学習環境を使用して、サンプルデータに対してK-means法やDBSCANを実装し、結果の可視化や評価を行うことで、理論と実践の橋渡しができます。

まとめ

クラスタリングは、データマイニングと機械学習の基礎技術として、現代の情報社会において極めて重要な役割を果たしています。K-means法、階層クラスタリング、DBSCAN、ガウス混合モデルなどの主要な手法は、それぞれ固有の特徴と適用場面を持ち、適切な選択と実装により強力な分析ツールとなります。

応用情報技術者試験においても重要なトピックであり、理論的理解と実践的応用能力の両方が求められます。基本概念から最新の発展まで幅広く学習し、実際のデータに対してクラスタリングを実行することで、深い理解と実践的なスキルを身につけることができます。

技術の進歩により、クラスタリングの応用範囲はますます広がっています。深層学習との融合、リアルタイム処理への対応、解釈性の向上、プライバシー保護など、様々な方向での発展が期待されます。これらの最新動向を継続的に学習し、実務に活用することで、データドリブンな意思決定と価値創造を実現できるでしょう。

クラスタリング技術を効果的に活用するためには、適切なツールと継続的な学習が不可欠です。実践的な経験を積み重ね、様々な分野での応用事例を学ぶことで、この強力な技術を最大限に活用できるようになります。

クラスタリング：データマイニングの基礎技術と実践的応用【2025年最新】