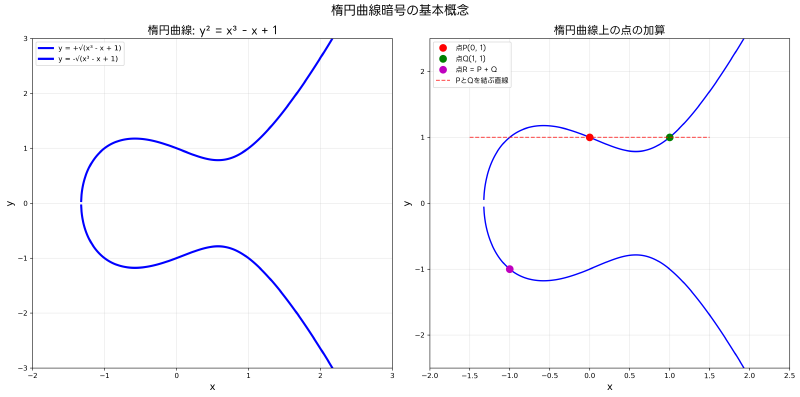
楕円曲線暗号(Elliptic Curve Cryptography、ECC)は、現代の情報セキュリティ分野において最も重要な暗号技術の一つです。従来のRSA暗号と比較して、同等のセキュリティレベルを短い鍵長で実現できるという革新的な特徴を持ち、モバイルデバイスやIoT機器などの資源制約のある環境での暗号化において特に威力を発揮します。応用情報技術者試験においても、現代暗号学の重要なトピックとして頻出の分野です。
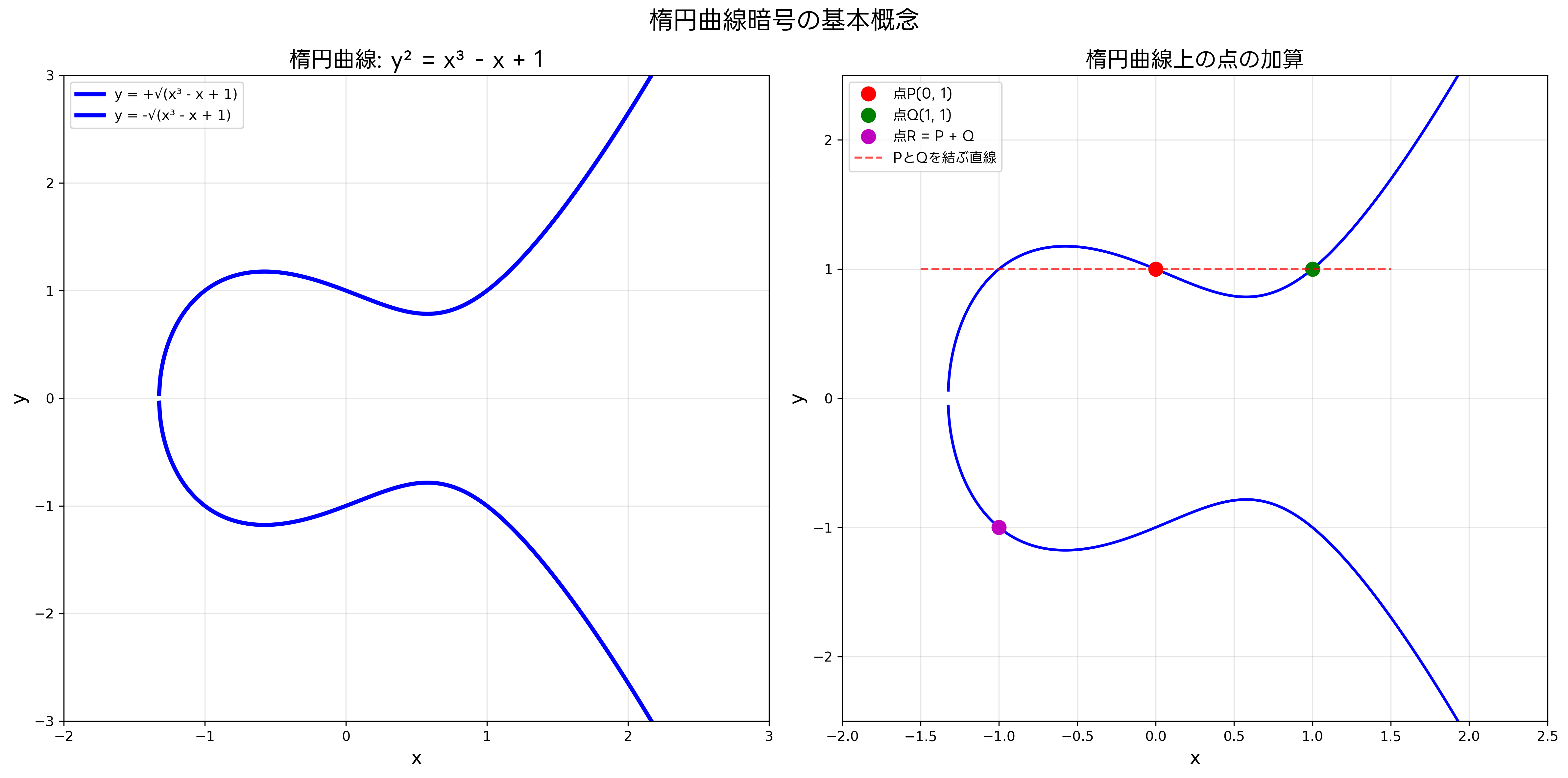
楕円曲線暗号は、楕円曲線上の点の加算という数学的操作に基づく離散対数問題の困難性を利用した公開鍵暗号システムです。この技術は1985年にVictor MillerとNeal Koblitzによって独立に提案され、以来、暗号学の分野で急速な発展を遂げています。
楕円曲線の数学的基礎
楕円曲線暗号の理解には、まず楕円曲線の数学的性質を理解することが重要です。楕円曲線は、Weierstrass形式では y² = x³ + ax + b という方程式で表現される代数曲線です。ここで、aとbは定数であり、判別式 4a³ + 27b² ≠ 0 という条件を満たす必要があります。この条件により、曲線が特異点を持たない滑らかな曲線であることが保証されます。
楕円曲線上の点には、特別な演算である点の加算が定義されています。二つの点P、Qが楕円曲線上にある場合、これらの点を結ぶ直線が曲線と交わる第三の点をRとすると、PとQの和はRのy座標の符号を反転させた点になります。この加算演算により、楕円曲線上の点の集合はアーベル群を形成します。
楕円曲線暗号においては、この点の加算を利用した離散対数問題が暗号の安全性の基盤となります。具体的には、楕円曲線上の基点をG、秘密鍵をk(整数)とすると、公開鍵は P = kG という点になります。Gと公開鍵Pが与えられたときに、秘密鍵kを求める問題が楕円曲線離散対数問題(ECDLP)と呼ばれ、これが計算困難であることがECCの安全性を支えています。
現実の暗号実装では、無限体上ではなく有限体上で楕円曲線を扱います。最も一般的なのは、素数pを法とする有限体Fp上での楕円曲線です。この場合、すべての計算はmod pで行われ、曲線上の点の数は有限となります。この有限性が実際のコンピュータでの実装を可能にしています。
RSA暗号との比較優位性
楕円曲線暗号の最大の利点は、RSA暗号と比較してはるかに短い鍵長で同等のセキュリティレベルを達成できることです。これは、楕円曲線離散対数問題の困難性が、RSA暗号の基盤となる整数因数分解問題よりも高いためです。
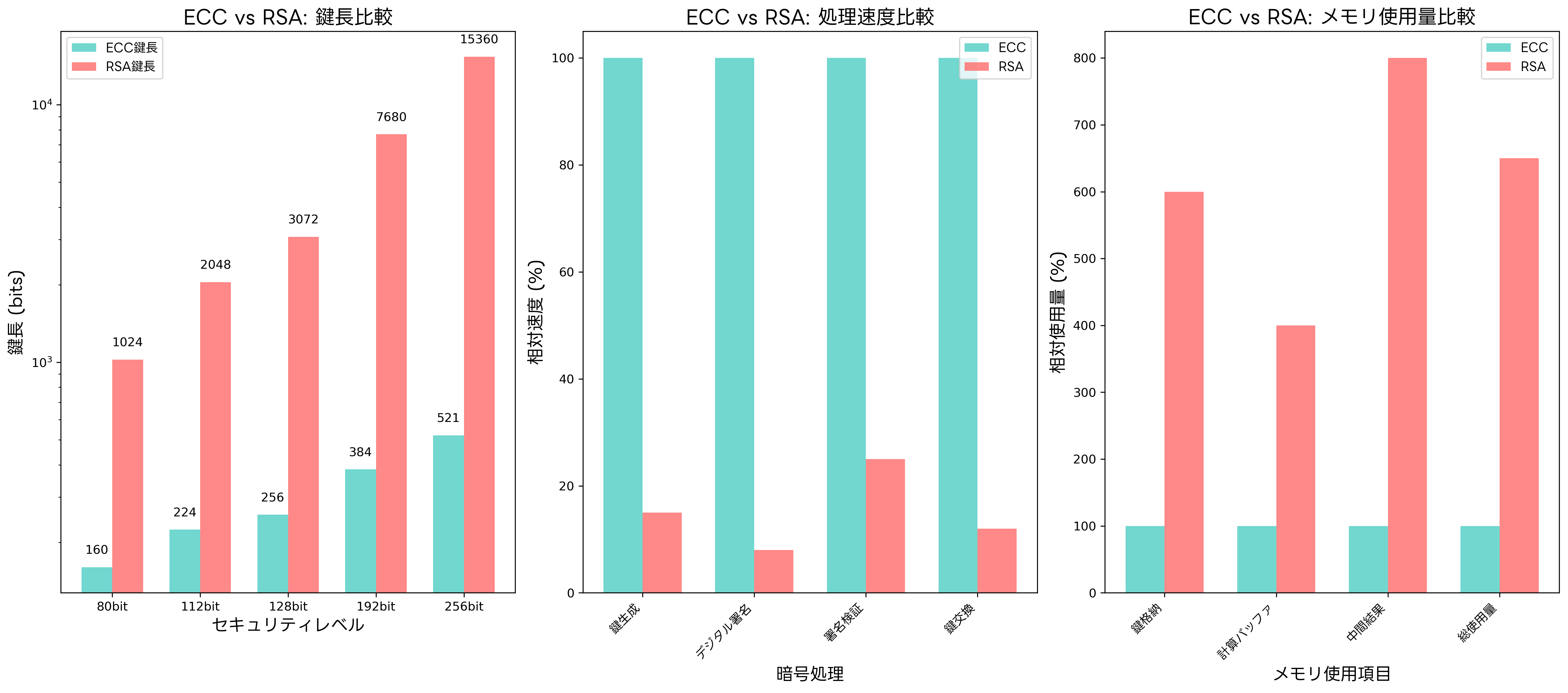
セキュリティレベル128bitを実現する場合、RSAでは3072bitの鍵長が必要ですが、ECCでは256bitの鍵長で十分です。これは約12分の1の鍵長であり、メモリ使用量、処理時間、通信帯域の大幅な節約を実現します。特に、モバイルデバイス向けセキュリティソリューションやIoTデバイス用暗号モジュールにおいて、この効率性は決定的な優位性となります。
計算性能の面でも、ECCはRSAを上回ります。鍵生成、デジタル署名、署名検証のすべての処理において、ECCの方が高速に実行できます。特に、バッテリー駆動のデバイスや処理能力が限られた組み込みシステムにおいて、この性能優位性は重要な意味を持ちます。高性能暗号処理チップを使用することで、ECCの性能をさらに向上させることも可能です。
メモリ使用量の観点でも、ECCは大きな利点を持ちます。短い鍵長により、鍵の保存に必要なメモリ領域が大幅に削減されるだけでなく、暗号処理に必要な作業メモリも少なくて済みます。これにより、メモリ制約のある組み込みシステムでも効率的な暗号化が実現できます。
通信効率の面では、短い鍵長により公開鍵の送信に必要な帯域が削減され、証明書のサイズも小さくなります。これは、帯域幅が限られたネットワーク環境や衛星通信システムにおいて特に重要な利点となります。
ECCの主要な応用分野
楕円曲線暗号は、現代の情報社会の様々な分野で広く活用されています。最も一般的な応用は、HTTPS通信におけるSSL/TLS証明書での利用です。WebブラウザとWebサーバー間の安全な通信を確立するために、ECCベースの証明書が広く採用されており、通信の暗号化と相互認証を効率的に実現しています。
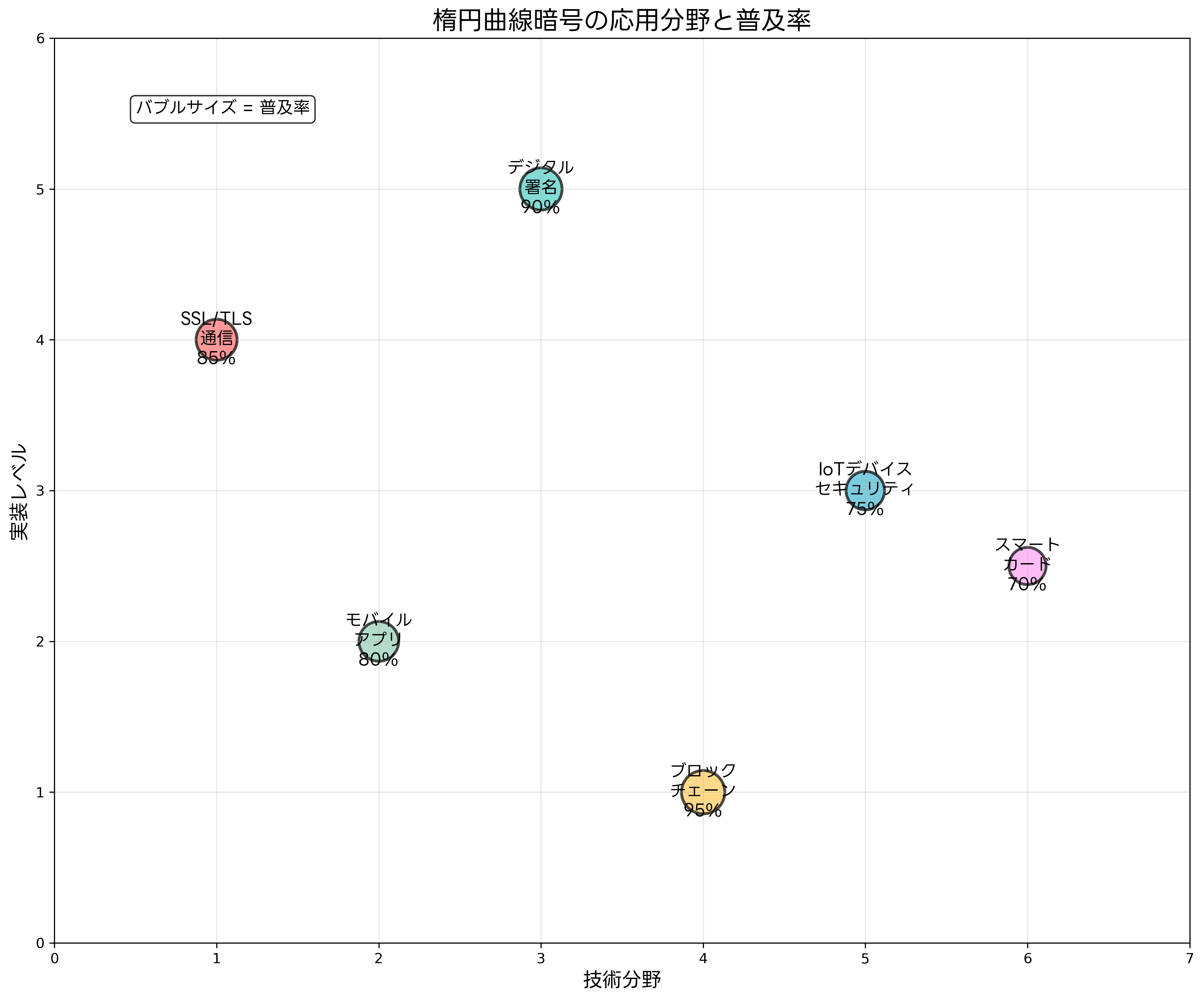
デジタル署名の分野では、ECDSA(Elliptic Curve Digital Signature Algorithm)が標準的に使用されています。電子契約、ソフトウェアの署名、電子メールのデジタル署名など、データの真正性と完全性を保証する用途で広く活用されています。デジタル署名ソフトウェアの多くがECCベースの署名機能を提供しています。
IoT(Internet of Things)デバイスのセキュリティにおいて、ECCは特に重要な役割を果たしています。センサーデバイス、スマートメーター、産業用制御システムなど、計算資源が限られた機器での暗号化において、ECCの効率性が不可欠です。IoTセキュリティゲートウェイや産業用IoTセキュリティソリューションにおいても、ECCが中核的な暗号技術として採用されています。
モバイルアプリケーションのセキュリティでも、ECCは重要な位置を占めています。スマートフォンアプリでの認証、データ保護、セキュアな通信において、バッテリー消費を抑えながら高いセキュリティを実現するために、ECCが活用されています。モバイルアプリセキュリティソリューションの多くがECCベースの暗号化機能を提供しています。
ブロックチェーン技術においても、ECCは欠かせない要素です。BitcoinやEthereumなどの暗号通貨では、ECCベースのデジタル署名により取引の署名と検証が行われています。また、スマートコントラクトや分散型アプリケーション(DApp)のセキュリティにおいても、ECCが重要な役割を果たしています。ブロックチェーン開発ツールや暗号通貨セキュリティソリューションにおいても、ECC技術が中核となっています。
スマートカードやICカードの分野では、限られた計算資源とメモリ容量の中で高度な暗号化を実現するために、ECCが広く採用されています。クレジットカード、身分証明書、交通系カードなど、日常生活で使用される多くのスマートカードがECCベースのセキュリティ機能を搭載しています。
標準楕円曲線の比較と選択
楕円曲線暗号の実装では、使用する楕円曲線の選択が重要な要素となります。現在、様々な標準化団体が推奨する楕円曲線が存在し、それぞれ異なる特性を持っています。最も広く使用されているのは、NIST(米国国立標準技術研究所)が推奨するP-256、P-384、P-521曲線です。
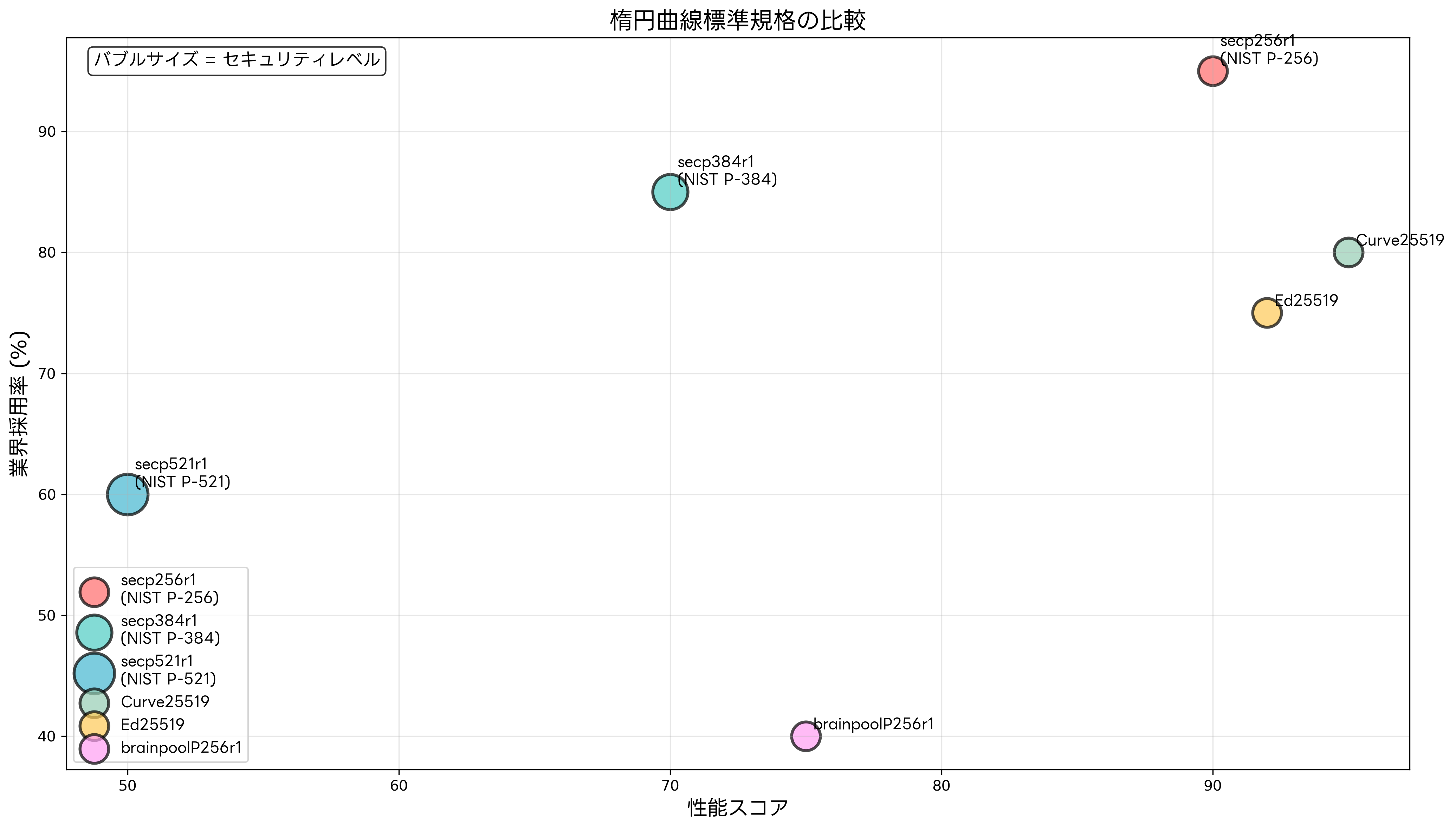
NIST P-256(secp256r1)は、256bitの鍵長でAESの128bitと同等のセキュリティレベルを提供し、現在最も広く採用されている楕円曲線です。SSL/TLS証明書、デジタル署名、暗号通貨など、幅広い用途で使用されています。バランスの取れた性能とセキュリティを提供するため、暗号ライブラリの多くがデフォルトでサポートしています。
Curve25519は、Dan Berensteinによって設計された楕円曲線で、特に高い性能と実装の安全性を重視して設計されています。Signal、WhatsApp、SSH などの暗号プロトコルで採用されており、サイドチャネル攻撃に対する耐性が高いという特徴があります。セキュア通信ライブラリでよく使用されています。
Ed25519は、デジタル署名に特化して最適化された楕円曲線で、非常に高速な署名生成と検証を実現します。Git、SSH、TLSなどの様々なプロトコルで採用されており、バージョン管理セキュリティツールでも広く使用されています。
brainpoolP256r1は、欧州の標準化団体によって設計された楕円曲線で、パラメータの生成過程が完全に公開されており、透明性が高いという特徴があります。欧州の政府機関や企業向けセキュリティソリューションで採用されることが多いです。
曲線の選択においては、セキュリティレベル、性能、実装の容易さ、標準化状況、特許の有無などを総合的に考慮する必要があります。また、使用する暗号ライブラリや開発環境での対応状況も重要な判断要素となります。
ECCのセキュリティ考慮事項
楕円曲線暗号の実装において、数学的な安全性だけでなく、実装レベルでのセキュリティも重要な課題となります。特に、サイドチャネル攻撃に対する対策は、実用的なECC実装において不可欠です。
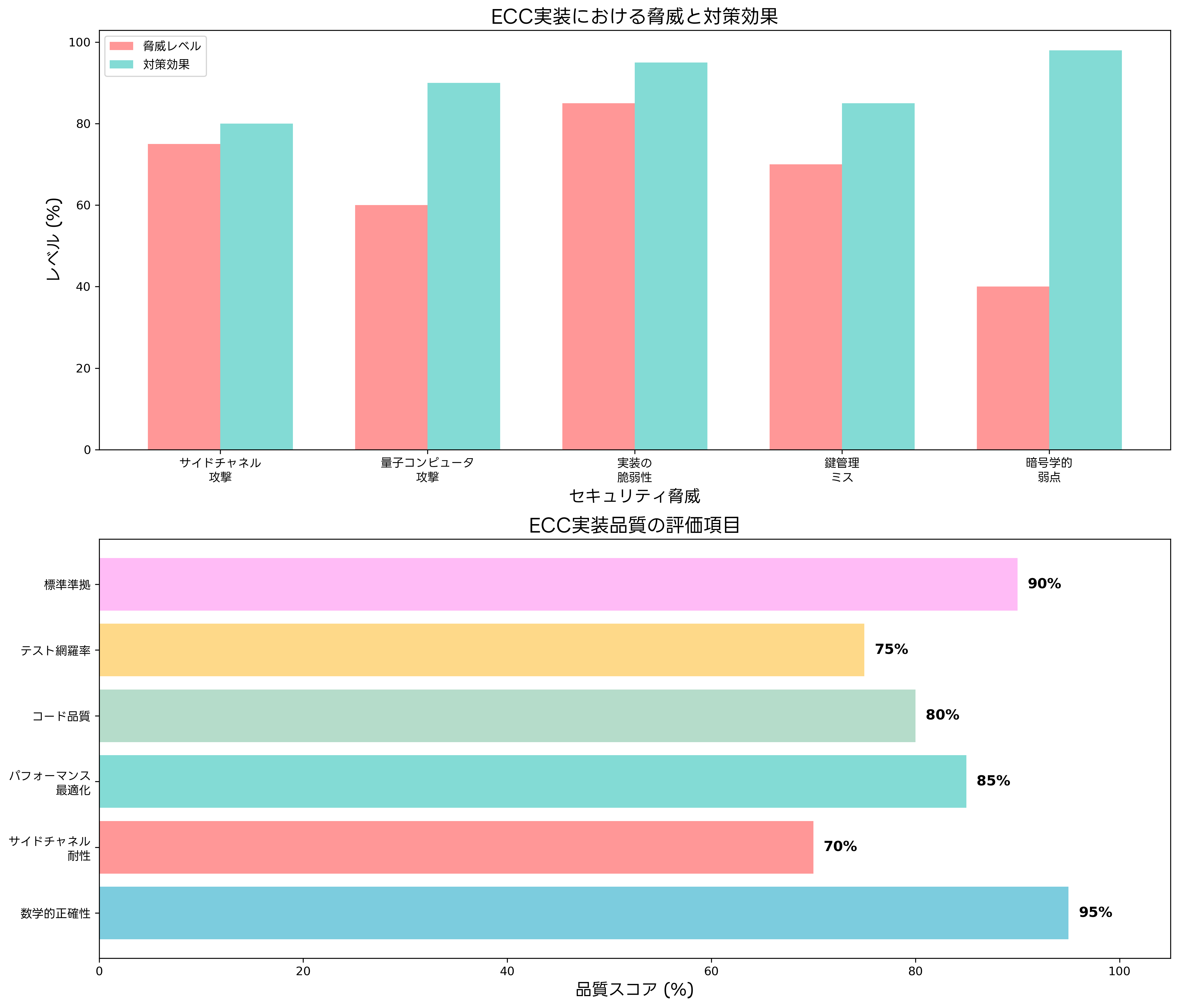
サイドチャネル攻撃は、暗号処理中に発生する消費電力、電磁波、処理時間などの副次的な情報を分析して秘密情報を推定する攻撃手法です。ECCの実装では、点の加算や倍算処理において、処理時間や消費電力が入力データに依存して変化する可能性があり、これが秘密鍵の漏洩につながる恐れがあります。サイドチャネル攻撃対策ツールを使用して、実装の安全性を検証することが重要です。
対策として、定時間実装(Constant-time Implementation)やマスキング技術が用いられます。定時間実装では、秘密データの値に関係なく常に同じ時間で処理を完了するように実装し、タイミング攻撃を防ぎます。マスキング技術では、秘密データをランダム値でマスクして処理することで、消費電力分析攻撃を困難にします。
量子コンピュータの脅威も、ECCにとって重要なセキュリティ考慮事項です。十分に大きな量子コンピュータが実現されると、Shorのアルゴリズムにより楕円曲線離散対数問題が多項式時間で解けるようになり、ECCの安全性が破綻する可能性があります。この脅威に対応するため、量子耐性暗号(Post-Quantum Cryptography)への移行準備が進められています。
実装の脆弱性も重要な課題です。ECCの数学的な操作は複雑であり、実装を誤ると重大な脆弱性が生じる可能性があります。例えば、無効曲線攻撃、ツイスト攻撃、フォルト攻撃などの手法により、不適切な実装から秘密鍵を抽出される危険があります。暗号実装検証ツールを使用して、実装の正確性と安全性を確認することが必要です。
鍵管理も重要なセキュリティ要素です。ECCでは短い鍵長により鍵の管理が簡素化されますが、適切な乱数生成、鍵の保存、鍵の更新、鍵の廃棄などのライフサイクル管理は依然として重要です。暗号鍵管理システムを使用して、組織全体での一元的な鍵管理を実現することが推奨されます。
ECCの実装技術と最適化
楕円曲線暗号の効率的な実装には、様々な数学的最適化技術が用いられます。最も基本的な最適化は、楕円曲線上の点演算の高速化です。点の加算や倍算処理において、射影座標系やJacobian座標系を使用することで、逆元演算の回数を削減し、全体的な処理速度を向上させることができます。
スカラー倍算の最適化では、バイナリ法、NAF(Non-Adjacent Form)法、ウィンドウ法などのアルゴリズムが使用されます。これらの手法により、秘密鍵kに対してkGを計算する際の点演算の回数を削減できます。特に、事前計算テーブルを使用するウィンドウ法は、メモリ使用量と処理速度のトレードオフを調整しながら、大幅な高速化を実現できます。
ハードウェアレベルでの最適化も重要です。専用暗号プロセッサやハードウェアセキュリティモジュール(HSM)を使用することで、ソフトウェア実装では実現できない高速性と安全性を同時に実現できます。
並列処理による最適化も可能です。複数のスカラー倍算を並列実行したり、楕円曲線の演算を複数のコアで分散処理したりすることで、スループットを向上させることができます。マルチコア暗号処理システムを活用することで、大量の暗号処理を効率的に実行できます。
ECCライブラリと開発環境
楕円曲線暗号を実際のシステムに実装する際には、信頼性の高い暗号ライブラリの選択が重要です。OpenSSLは最も広く使用されているオープンソースの暗号ライブラリで、様々な楕円曲線と暗号プリミティブをサポートしています。商用システムでは、商用暗号ライブラリを使用することで、技術サポートとセキュリティ保証を得ることができます。
組み込みシステム向けには、軽量化された暗号ライブラリが重要です。mbedTLS、WolfSSL、micro-eccなどのライブラリは、メモリ使用量と処理速度を最適化して、資源制約のある環境でのECC実装を可能にします。組み込みシステム開発キットの多くがこれらのライブラリをサポートしています。
セキュリティテストと検証も重要な要素です。暗号プロトコル検証ツールやセキュリティテスト自動化ツールを使用して、実装されたECCシステムの安全性と正確性を継続的に検証することが必要です。
応用情報技術者試験での出題傾向
応用情報技術者試験において、楕円曲線暗号は現代暗号学の重要なトピックとして出題されています。午前問題では、ECCの基本概念、RSAとの比較、鍵長とセキュリティレベルの関係、応用分野などについて問われることが多いです。
特に頻出なのは、同等のセキュリティレベルを実現するためのECCとRSAの鍵長比較問題です。「AESの128bitセキュリティと同等の安全性を実現するために必要な鍵長は、RSAでは何bitか、ECCでは何bitか」といった具体的な数値を問う問題が出題されます。応用情報技術者試験対策書で、これらの関係性を正確に理解することが重要です。
午後問題では、より実践的な観点からECCの活用が問われます。システム設計における暗号方式の選択、性能とセキュリティのトレードオフ、実装上の考慮事項などが出題される傾向があります。実際のシステム開発経験や暗号技術実践書での学習により、理論と実践を結びつけた理解を深めることが有効です。
将来の展望と新技術
楕円曲線暗号の分野では、量子コンピュータ時代に向けた新たな技術開発が活発に行われています。量子耐性を持つ楕円曲線の研究、楕円曲線以外の代数的構造を利用した暗号方式、ハイブリッド暗号システムなどが注目されています。
同型暗号や零知識証明との組み合わせにより、プライバシー保護計算やブロックチェーンのスケーラビリティ問題の解決にECCが活用される可能性も期待されています。プライバシー保護技術やブロックチェーンスケーリングソリューションにおいて、ECCベースの新技術が重要な役割を果たすと予想されます。
エッジコンピューティングや5G通信の普及により、ECCの適用分野はさらに拡大しています。エッジコンピューティングセキュリティや5Gネットワークセキュリティにおいて、ECCの効率性と安全性が重要な要素となっています。
まとめ
楕円曲線暗号は、現代の情報セキュリティにおいて不可欠な技術として確立されています。RSAと比較して短い鍵長で同等のセキュリティを実現できる効率性、モバイルデバイスやIoT機器での優れた性能、様々な暗号プリミティブでの幅広い応用性など、多くの優位性を持っています。
応用情報技術者試験においても重要なトピックであり、理論的な理解と実践的な応用能力の両方が求められます。数学的基礎から実装技術、セキュリティ考慮事項まで、幅広い知識を体系的に身につけることが重要です。
技術の進歩とともに、ECCの応用分野はますます拡大しており、量子コンピュータ時代に向けた新たな展開も期待されています。継続的な学習と実践により、変化する技術環境に対応できる専門性を身につけることが、情報セキュリティ分野での成功につながるでしょう。