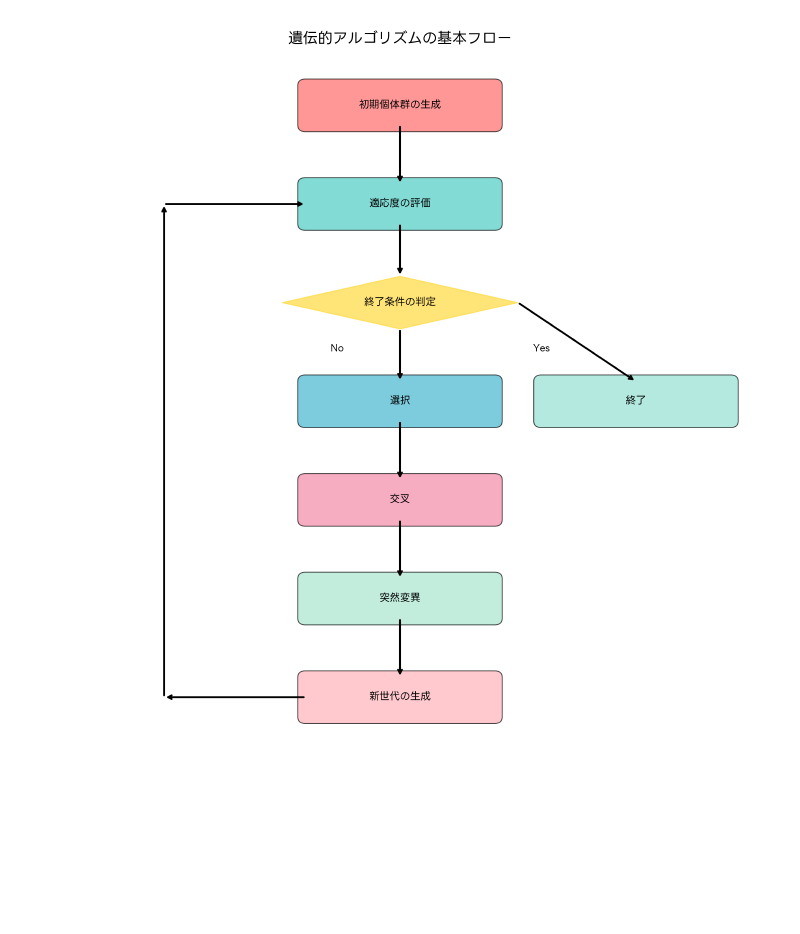
遺伝的アルゴリズム：生物進化を模倣した最適化手法

遺伝的アルゴリズム（Genetic Algorithm, GA）は、生物の進化過程を模倣した最適化アルゴリズムとして、1970年代にジョン・ホランド（John Holland）によって提案されました。この手法は、自然淘汰、遺伝、突然変異といった生物学的概念を計算機科学に応用し、複雑な最適化問題を効率的に解決する強力なツールとして広く利用されています。応用情報技術者試験においても重要なトピックであり、人工知能やメタヒューリスティクス分野の基礎知識として必須の概念です。

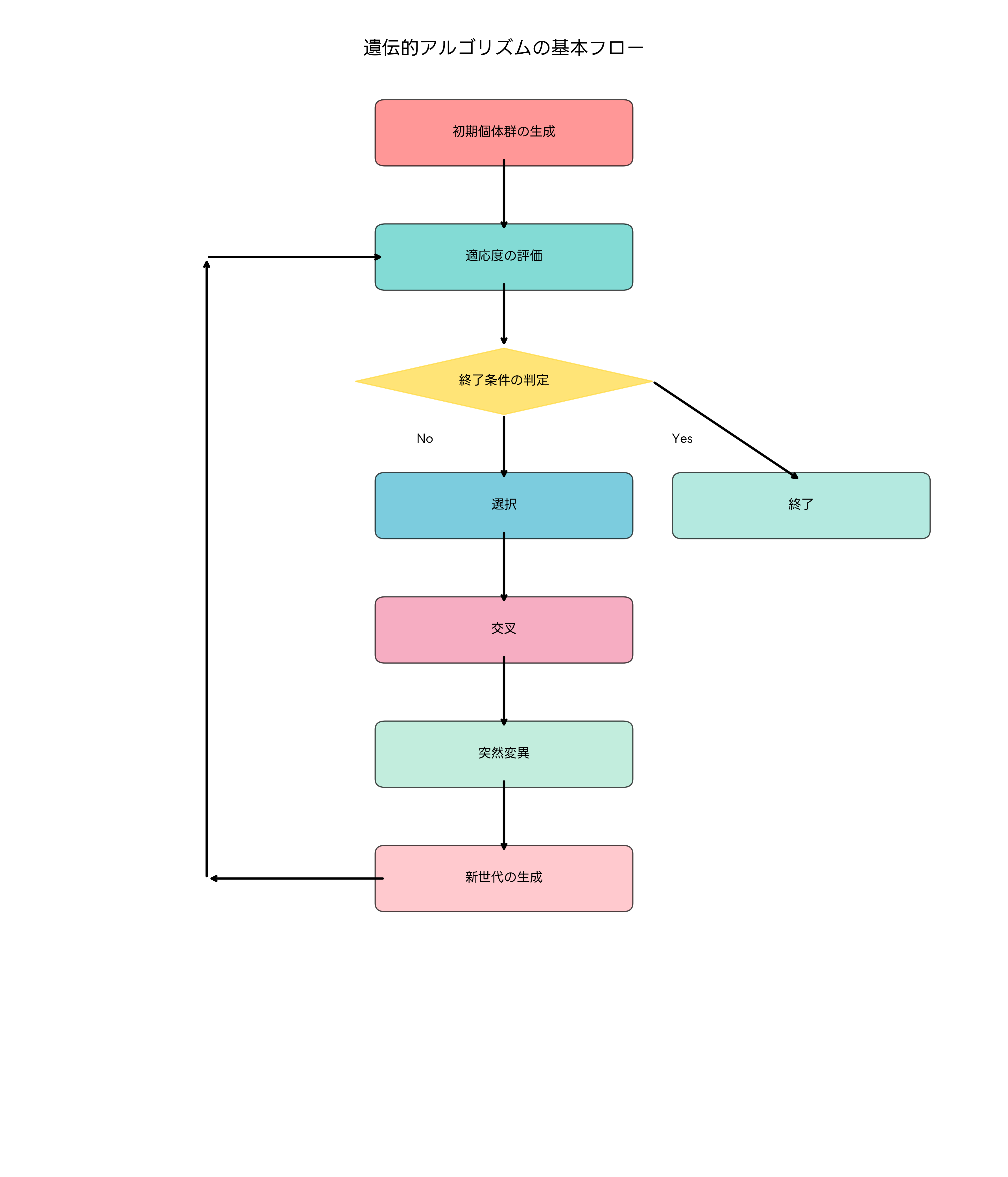
遺伝的アルゴリズムの基本フロー

遺伝的アルゴリズムの核心は、解の候補を「個体」として表現し、これらの個体群を「世代」を重ねながら進化させることで、より良い解を探索することにあります。各個体は遺伝子（chromosome）として符号化され、適応度（fitness）によって評価されます。優秀な個体ほど次世代に遺伝子を残しやすくなり、交叉（crossover）と突然変異（mutation）を通じて新しい個体が生成されます。

遺伝的アルゴリズムの基本構成要素

遺伝的アルゴリズムを構成する基本要素を理解することは、効果的な実装と運用のために不可欠です。まず、個体の表現方法（符号化）が重要な要素となります。最も一般的なのは二進符号化で、解を0と1のビット列として表現します。この方法は実装が簡単で、多くの問題に適用できるため、プログラミング学習教材でも頻繁に使用されます。

実数符号化は、実数値の最適化問題に適しており、連続的な解空間を直接扱えます。順列符号化は、巡回セールスマン問題やスケジューリング問題など、順序が重要な問題に使用されます。木構造符号化は、遺伝的プログラミングで使用され、プログラムや数式の進化に応用されます。これらの符号化方法を学習するためには、アルゴリズム専門書が有効です。

適応度関数は、各個体の良さを数値で評価する関数です。問題の目的に応じて設計され、最大化問題では高い値を、最小化問題では低い値を良い解として扱います。適応度関数の設計は遺伝的アルゴリズムの性能に直結するため、問題の性質を深く理解することが重要です。適応度の設計に関する詳細な解説は、最適化理論の教科書で学習できます。

個体群のサイズも重要なパラメータです。個体数が少なすぎると多様性が不足し、局所最適解に陥りやすくなります。逆に個体数が多すぎると計算コストが増大し、収束に時間がかかります。一般的には、問題の複雑さに応じて50から500個体程度が使用されることが多く、実際の運用では高性能計算機を使用して大規模な個体群を扱うこともあります。

選択操作：優秀な個体の選び方

選択操作は、次世代に遺伝子を残す親個体を決定する重要な処理です。自然界の自然淘汰を模倣し、適応度の高い個体ほど選ばれやすくなるよう設計されています。選択方法にはいくつかの手法があり、それぞれ異なる特性を持ちます。

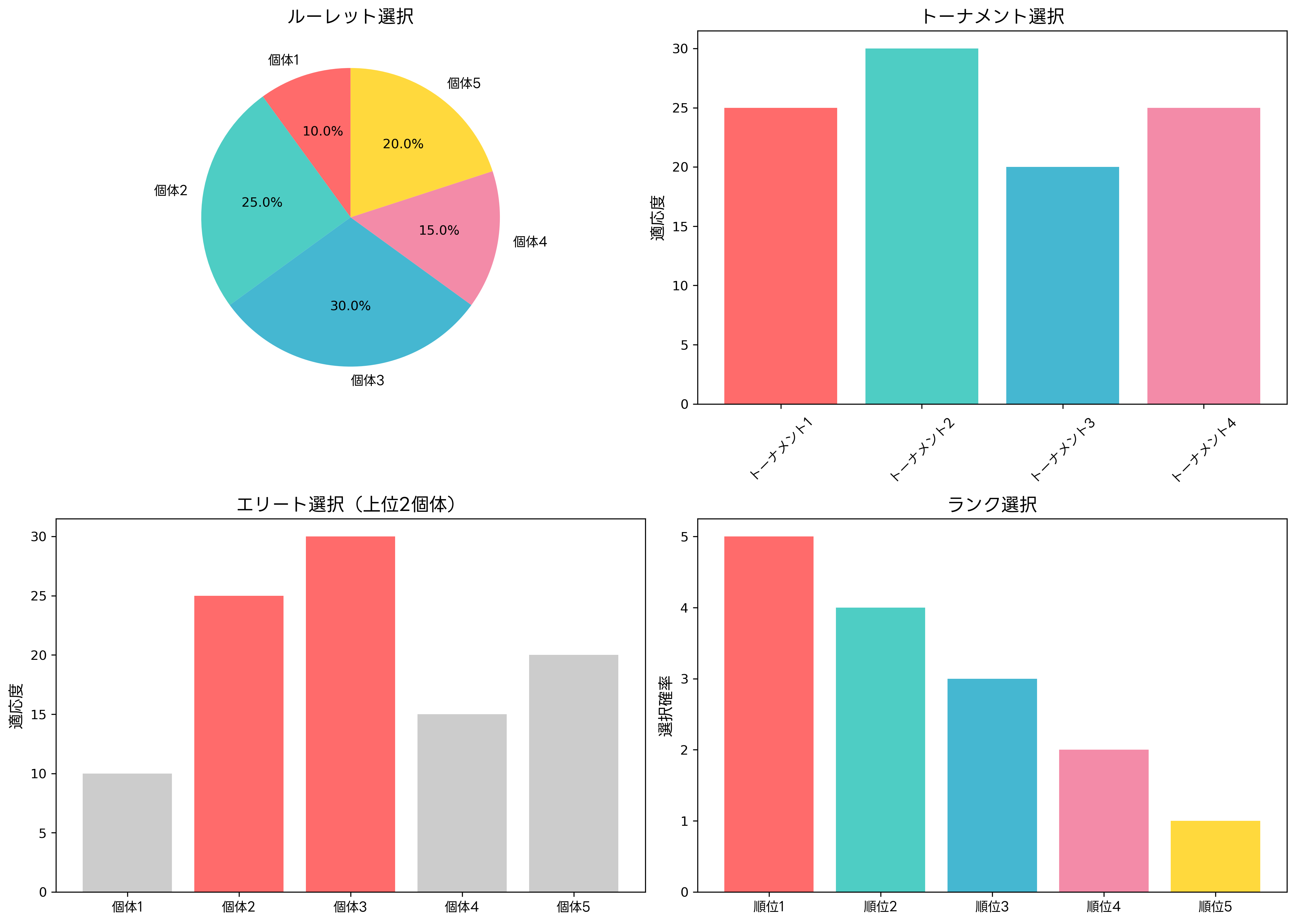
選択方法の比較

ルーレット選択は最も直感的な選択方法で、各個体の適応度に比例した確率で選択されます。ルーレットを回すように、適応度の高い個体ほど大きな領域を占め、選ばれやすくなります。この方法は実装が簡単で理解しやすいため、遺伝的アルゴリズムの入門書やプログラミング演習教材でよく紹介されます。

トーナメント選択は、個体群からランダムに選んだ複数の個体でトーナメントを行い、その中で最も適応度の高い個体を選ぶ方法です。トーナメントサイズを調整することで選択圧を調整でき、実装も比較的簡単です。この方法は適応度の分布に依存しないため、負の適応度を持つ問題にも適用できます。

エリート選択は、現世代で最も優秀な個体を確実に次世代に残す方法です。最良解の消失を防ぎ、単調な改善を保証しますが、多様性の減少を招く可能性があります。通常は他の選択方法と組み合わせて使用され、個体群の一部（1-10%程度）にエリート選択を適用します。

ランク選択は、個体を適応度順にランク付けし、そのランクに基づいて選択確率を決定します。適応度の絶対値ではなく相対的な順位を使用するため、適応度の分布に影響されにくい特徴があります。また、世代が進むにつれて個体間の適応度差が小さくなっても、安定した選択圧を維持できます。実際の最適化ソフトウェアでは、これらの選択方法を組み合わせて使用することが一般的です。

交叉操作：遺伝情報の組み合わせ

交叉操作は、選択された親個体の遺伝情報を組み合わせて新しい個体を生成する操作です。生物学の有性生殖を模倣しており、親の持つ良い特徴を子に受け継がせることで、解の品質向上を図ります。交叉方法は符号化方式によって異なり、問題の性質に応じて適切な手法を選択する必要があります。

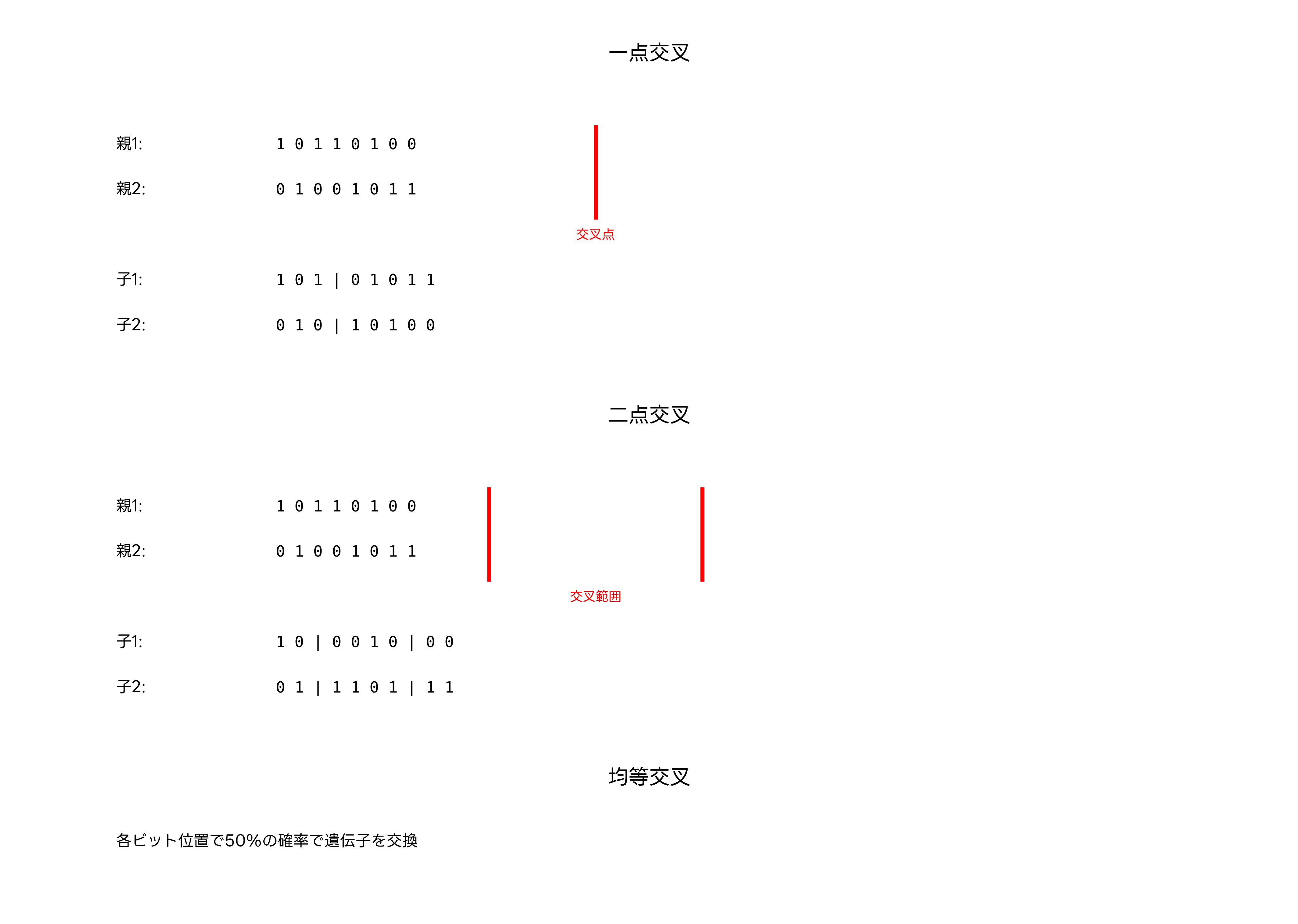
交叉方法の例

一点交叉は最も基本的な交叉方法で、遺伝子列の一点で切断し、前半と後半を入れ替えます。実装が簡単で、多くの問題に適用できるため、遺伝的アルゴリズムの学習において最初に習得する手法です。アルゴリズム実装書では、この手法から詳しく解説されることが多いです。

二点交叉は、遺伝子列の二点で切断し、中間部分を交換する方法です。一点交叉よりも多様な子個体を生成でき、遺伝子の位置効果を軽減できます。特に、遺伝子間の関係性が重要な問題では、二点交叉の方が良い結果を得られることがあります。

均等交叉は、各遺伝子位置で独立に親のどちらから遺伝子を受け継ぐかを決定します。従来の一点・二点交叉とは異なり、連続した遺伝子ブロックの概念がありません。この方法は高い探索能力を持ちますが、有用な遺伝子ブロックを破壊する可能性もあります。

実数符号化の場合は、算術交叉やブレンド交叉などの手法が使用されます。算術交叉は親の値の加重平均を計算し、ブレンド交叉は親の値の周辺で乱数を生成します。これらの手法は連続最適化問題で効果的で、数値計算ライブラリとして実装されていることもあります。

順列符号化では、部分的に対応する交叉（PMX）、順序交叉（OX）、循環交叉（CX）などが使用されます。これらは順列の制約を満たしながら遺伝情報を組み合わせる必要があり、巡回セールスマン問題やスケジューリング問題で重要です。

突然変異操作：多様性の保持

突然変異操作は、個体の遺伝子をランダムに変更する操作で、個体群の遺伝的多様性を保持し、局所最適解からの脱出を可能にします。生物学の突然変異を模倣しており、一般的に低い確率（0.1-5%程度）で実行されます。交叉操作が個体群内の既存の遺伝情報を組み合わせるのに対し、突然変異は新しい遺伝情報を導入する役割を果たします。

二進符号化では、ビット反転突然変異が最も一般的です。各ビットに対して突然変異確率に従って0を1に、1を0に反転させます。この操作は実装が簡単で、理論的な解析も容易なため、遺伝的アルゴリズム理論書でよく用いられます。

実数符号化では、ガウス突然変異がよく使用されます。現在の値に正規分布に従う乱数を加算することで、新しい値を生成します。分散パラメータを調整することで、突然変異の強度を制御できます。世代が進むにつれて分散を小さくする適応的突然変異も提案されており、局所探索の精度を向上させます。

順列符号化では、交換突然変異、挿入突然変異、逆転突然変異などが使用されます。交換突然変異は2つの要素の位置を交換し、挿入突然変異は要素を別の位置に移動させ、逆転突然変異は部分列を逆順にします。これらの操作は順列の制約を保持しながら変更を加えるため、組み合わせ最適化問題で重要です。

突然変異率の設定は遺伝的アルゴリズムの性能に大きく影響します。率が低すぎると多様性が不足し、高すぎるとランダム探索に近くなってしまいます。動的に突然変異率を調整する適応的手法も研究されており、最新の研究動向として注目されています。

適応度の評価と進化の監視

適応度の評価は遺伝的アルゴリズムの核心部分であり、解の品質を定量的に測定する重要な処理です。適応度関数の設計は問題に依存し、単純な数学的最適化から複雑な工学設計問題まで、幅広い分野で異なるアプローチが取られます。効果的な適応度関数は、真の目的を正確に反映し、計算効率が良く、微分可能であることが望ましいとされています。

適応度の変化

多目的最適化では、複数の目的関数を同時に考慮する必要があります。パレート最適性の概念を導入し、支配関係に基づいて個体を評価します。NSGA-II（Non-dominated Sorting Genetic Algorithm II）やMOEA/D（Multi-Objective Evolutionary Algorithm based on Decomposition）などの手法が開発されており、多目的最適化専門書で詳しく解説されています。

制約条件がある問題では、制約違反をペナルティ関数で扱ったり、実行可能解と実行不可能解を区別して評価したりします。制約の扱い方は問題の成功に直結するため、慎重な設計が必要です。実際の工学問題では、制約最適化ソフトウェアが使用されることも多く、専門的な知識が要求されます。

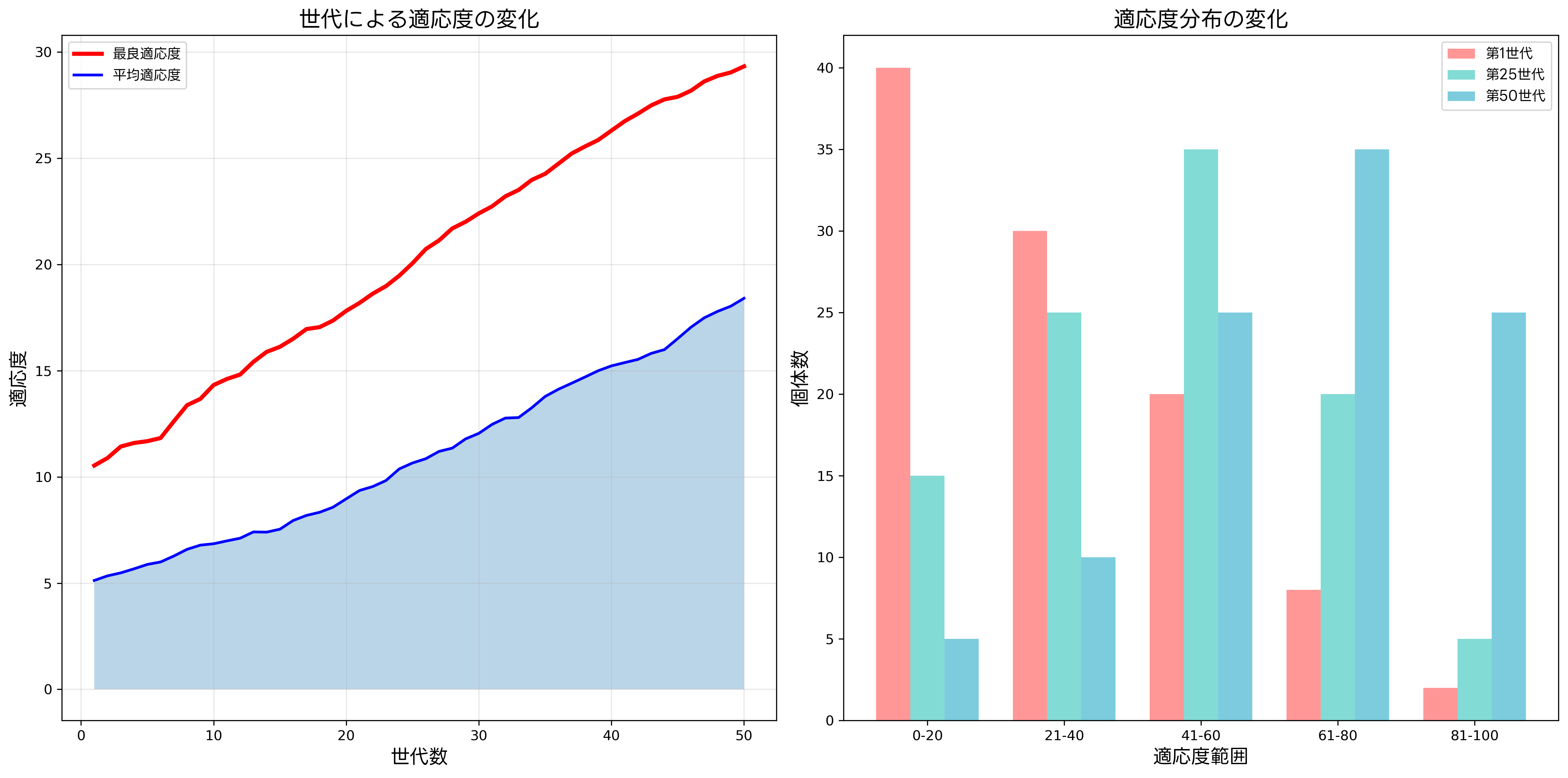
進化の監視では、最良適応度、平均適応度、適応度の分散などの統計情報を追跡します。これらの指標により、アルゴリズムの収束状況や多様性の変化を把握できます。早期収束の検出や停止条件の設定にも利用され、効率的な最適化の実現に不可欠です。

適応度の可視化とモニタリングのために、データ可視化ツールや統計解析パッケージが活用されます。特に、複雑な実問題では進化過程の理解が重要であり、適切な可視化によって洞察を得ることができます。

パラメータ調整と性能最適化

遺伝的アルゴリズムの性能は、各種パラメータの設定に大きく依存します。個体群サイズ、交叉率、突然変異率、世代数、エリート保存率などの主要パラメータを適切に調整することで、問題に対する最適化性能を大幅に向上させることができます。

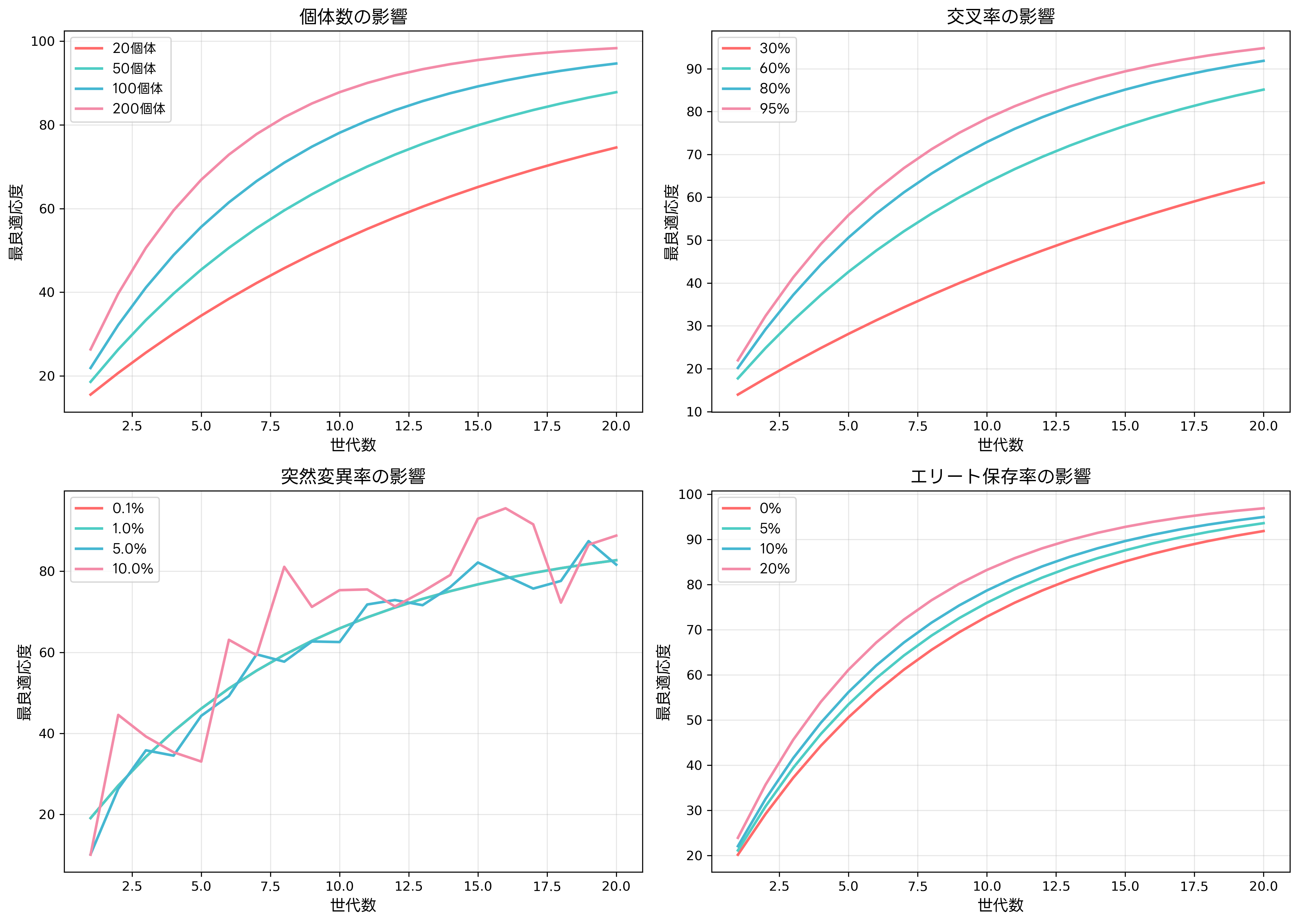
パラメータの影響比較

個体群サイズは探索の広さと計算コストのトレードオフを決定します。小さすぎる個体群は多様性不足により早期収束を引き起こし、大きすぎる個体群は計算時間の増大を招きます。一般的には、問題の次元数の10-50倍程度が目安とされますが、問題の性質により大きく異なります。実際の設定では、ベンチマーク問題集を用いて予備実験を行うことが重要です。

交叉率は一般的に60-95%程度に設定されます。高い交叉率は探索の強化につながりますが、良い個体の破壊リスクも高まります。問題の性質や符号化方式によって最適値は変わるため、パラメータスイープによる調整が必要です。パラメータ最適化ツールを使用することで、効率的な調整が可能になります。

突然変異率は通常1/L（Lは遺伝子長）程度に設定されますが、問題により大きく異なります。適応的突然変異では、進化の進行に応じて動的に調整されます。初期は高い突然変異率で探索を行い、収束に近づくにつれて局所探索を強化するアプローチが効果的です。

エリート保存は最良解の保持を保証しますが、多様性の減少を招く可能性があります。通常、個体群の1-10%程度を保存しますが、問題の複雑さに応じて調整が必要です。複数のエリートを保存する多重エリート戦略も提案されており、多様性と収束性のバランスを取ることができます。

応用分野と実際の適用例

遺伝的アルゴリズムは、その汎用性と堅牢性により、工学、経営、科学研究など幅広い分野で応用されています。特に、従来の数学的最適化手法では扱いが困難な複雑な問題において、その威力を発揮します。

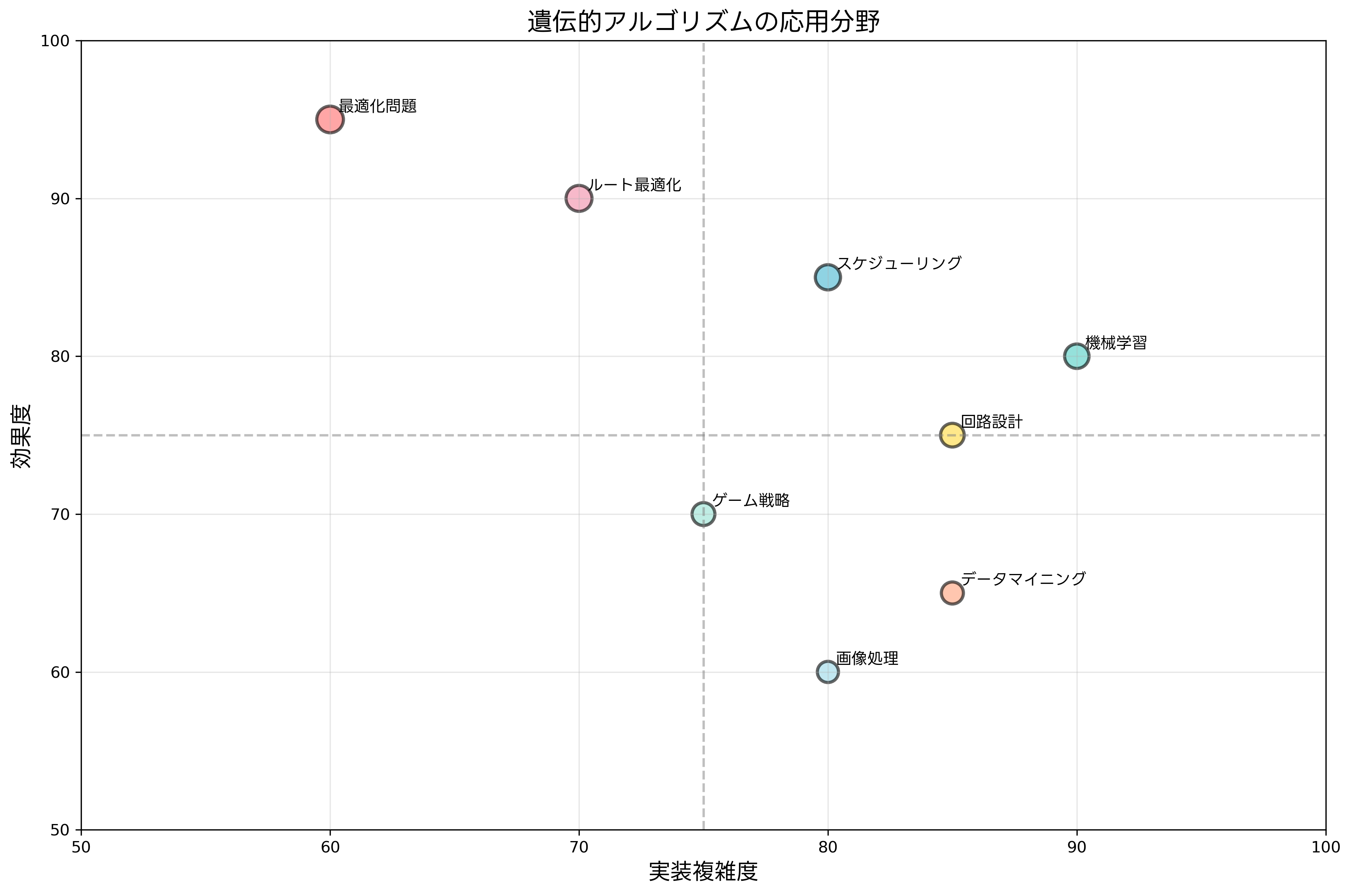
応用分野の比較

スケジューリング問題は遺伝的アルゴリズムの代表的な応用分野です。工場の生産スケジュール、学校の時間割作成、看護師のシフト表作成など、多くの制約条件を満たしながら最適なスケジュールを生成します。これらの問題は通常NP困難であり、厳密解を求めることは実用的でないため、遺伝的アルゴリズムのような近似手法が重宝されます。実際の運用では、スケジューリングソフトウェアに組み込まれることが多いです。

ルート最適化では、巡回セールスマン問題（TSP）や配送ルート最適化（VRP）が代表例です。物流業界では、燃料費の削減や配送時間の短縮が直接的な利益につながるため、高精度な最適化が求められます。大規模な問題では、ハイブリッド手法として局所探索を組み合わせることで、さらなる性能向上が図られます。物流最適化システムでは、リアルタイムの交通情報と組み合わせた動的最適化も実現されています。

機械学習分野では、ニューラルネットワークの構造最適化、特徴選択、ハイパーパラメータ調整などに応用されています。従来の勾配法では最適化が困難な離散的なパラメータや、微分不可能な目的関数に対して有効です。近年では、AutoMLの文脈で注目され、機械学習プラットフォームに組み込まれることが増えています。

回路設計やVLSI設計では、回路の配置配線問題、論理回路の最適化、アナログ回路のパラメータ調整などに利用されています。これらの問題は高次元で複雑な制約を持つため、遺伝的アルゴリズムの堅牢性が重要です。回路設計CADツールでは、従来の手法と組み合わせることで実用的な性能を実現しています。

金融工学では、ポートフォリオ最適化、リスク管理、デリバティブ価格決定などに応用されています。市場の不確実性や非線形性を考慮した最適化において、遺伝的アルゴリズムの探索能力が活用されます。金融工学ソフトウェアでは、リアルタイムの市場データと組み合わせた動的最適化が実現されています。

応用情報技術者試験での出題傾向

応用情報技術者試験において、遺伝的アルゴリズムは人工知能分野の重要なトピックとして頻繁に出題されています。午前問題では、基本概念、アルゴリズムの流れ、主要な操作（選択、交叉、突然変異）、パラメータの影響などが問われます。特に、生物学的概念との対応関係や、他の最適化手法との比較が重要なポイントです。

午後問題では、より実践的な場面での遺伝的アルゴリズムの適用が問われます。具体的な問題設定において、適切な符号化方式の選択、適応度関数の設計、パラメータの調整方針などが評価されます。また、アルゴリズムの性能評価や改善提案も重要な観点です。

試験対策としては、基本概念の理解に加えて、具体的な適用例を通じて実践的な知識を身につけることが重要です。応用情報技術者試験対策書では、遺伝的アルゴリズムの章が詳しく解説されており、過去問題の分析も含まれています。

また、実際にプログラムを作成して動作を確認することで、理論と実践の両面から理解を深めることができます。プログラミング演習書やオンライン学習プラットフォームを活用することで、効率的な学習が可能です。

関連する他のメタヒューリスティクス手法（粒子群最適化、シミュレーテッドアニーリング、タブー探索など）との比較も重要な観点です。それぞれの手法の特徴と適用場面を理解することで、問題に応じた手法選択の判断力を養うことができます。

まとめ

遺伝的アルゴリズムは、生物進化の原理を巧妙に模倣した強力な最適化手法として、理論と実践の両面で重要な地位を占めています。その汎用性と堅牢性により、工学、経営、科学研究など幅広い分野で成功を収めており、今後もさらなる発展が期待されます。

応用情報技術者試験においては、人工知能分野の基礎知識として重要であり、基本概念から実践的な応用まで幅広い理解が求められます。理論的な背景を理解し、具体的な問題への適用方法を習得することで、実務でも活用できる知識を身につけることができます。

現代のデジタル社会において、最適化問題はますます複雑化し、大規模化しています。遺伝的アルゴリズムは、このような課題に対する有効なソリューションの一つとして、継続的な研究と開発が進められています。新しい技術との融合により、さらに高性能で実用的なアルゴリズムの開発が期待され、未来の情報社会を支える重要な技術として発展していくでしょう。

遺伝的アルゴリズム：生物進化を模倣した最適化手法【2025年最新】