インターバルという概念は、数学、コンピュータサイエンス、統計学、そして応用情報技術者試験においても重要な役割を果たしています。区間や時間的な間隔を表現するこの概念は、データ構造、アルゴリズム、数値計算、スケジュール管理など、様々な分野で活用されています。本記事では、インターバルの基本概念から実用的な応用まで、包括的に解説します。
インターバルの基本概念と数学的定義
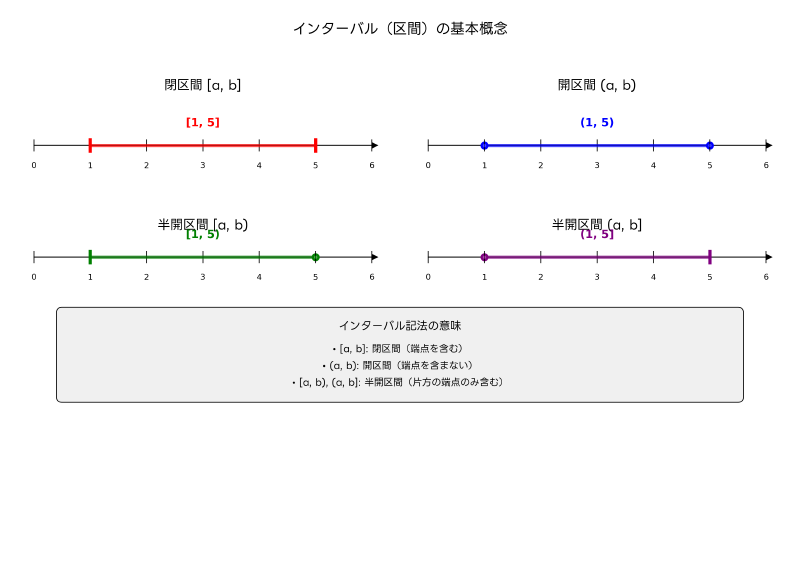
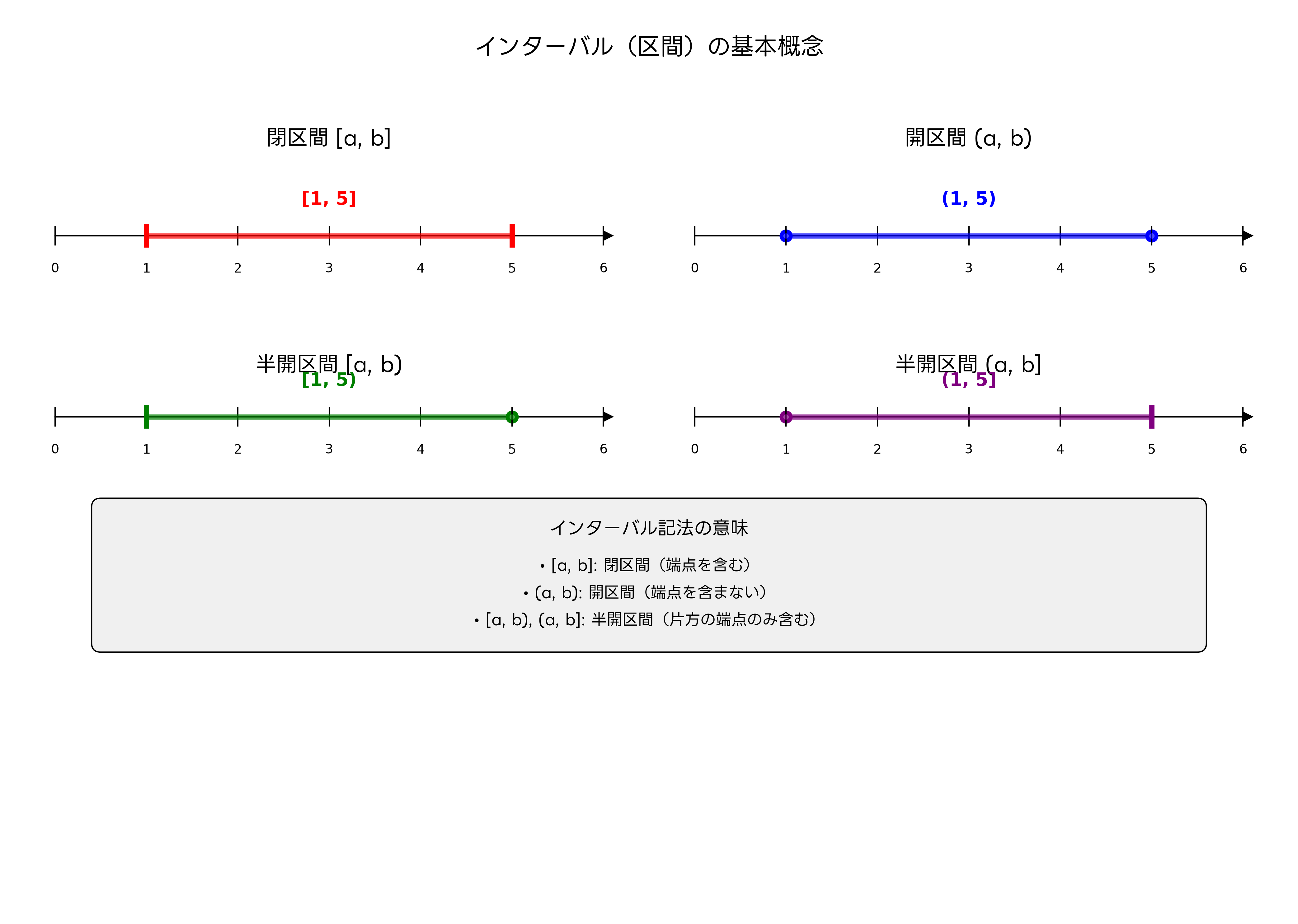
インターバルとは、数学において連続する数値の範囲を表現する概念です。実数直線上の二つの点によって定義される区間を指し、開区間、閉区間、半開区間という三つの主要な形式があります。この概念は、不確実性を含む数値計算や範囲を持つデータの処理において極めて重要な役割を果たします。
閉区間[a, b]は、端点aとbを含む区間を表します。これは、a以上b以下のすべての実数を含む集合として定義されます。例えば、[1, 5]という閉区間は、1から5までのすべての実数を含み、端点である1と5も含まれます。この記法は、製造業における品質管理で製品の仕様範囲を定義する際によく使用され、高精度計測器による測定結果の許容範囲を表現するのに適しています。
開区間(a, b)は、端点を含まない区間を表します。この場合、aより大きくbより小さいすべての実数が含まれますが、aとb自体は含まれません。例えば、(0, 1)という開区間は、0と1を除く0から1の間のすべての実数を含みます。この概念は、極限値の計算や連続性の定義において重要であり、数値解析ソフトウェアでの計算精度の指定に使用されることがあります。
半開区間は、片方の端点のみを含む区間です。[a, b)は左端点aを含み右端点bを含まない区間、(a, b]は左端点aを含まず右端点bを含む区間を表します。この記法は、プログラミングにおける配列のインデックス範囲の指定や、時間間隔の定義で特に有用です。例えば、[0, 10)は0以上10未満の範囲を表し、多くのプログラミング言語でのループ処理の範囲指定と一致します。
インターバル算術は、区間を含む計算を体系化した数学的手法です。通常の算術演算を区間に拡張したもので、不確実性や誤差を含む計算において威力を発揮します。この手法により、計算結果の信頼性を数学的に保証できるため、科学技術計算ソフトウェアや工学シミュレーションツールで広く採用されています。
インターバル演算と数値計算への応用
インターバル演算は、通常の算術演算を区間に対して拡張した演算体系です。この演算により、計算過程で発生する丸め誤差や測定誤差を厳密に追跡し、最終結果の信頼性を保証することができます。現代の高精度計算が要求される分野において、この手法の重要性はますます高まっています。
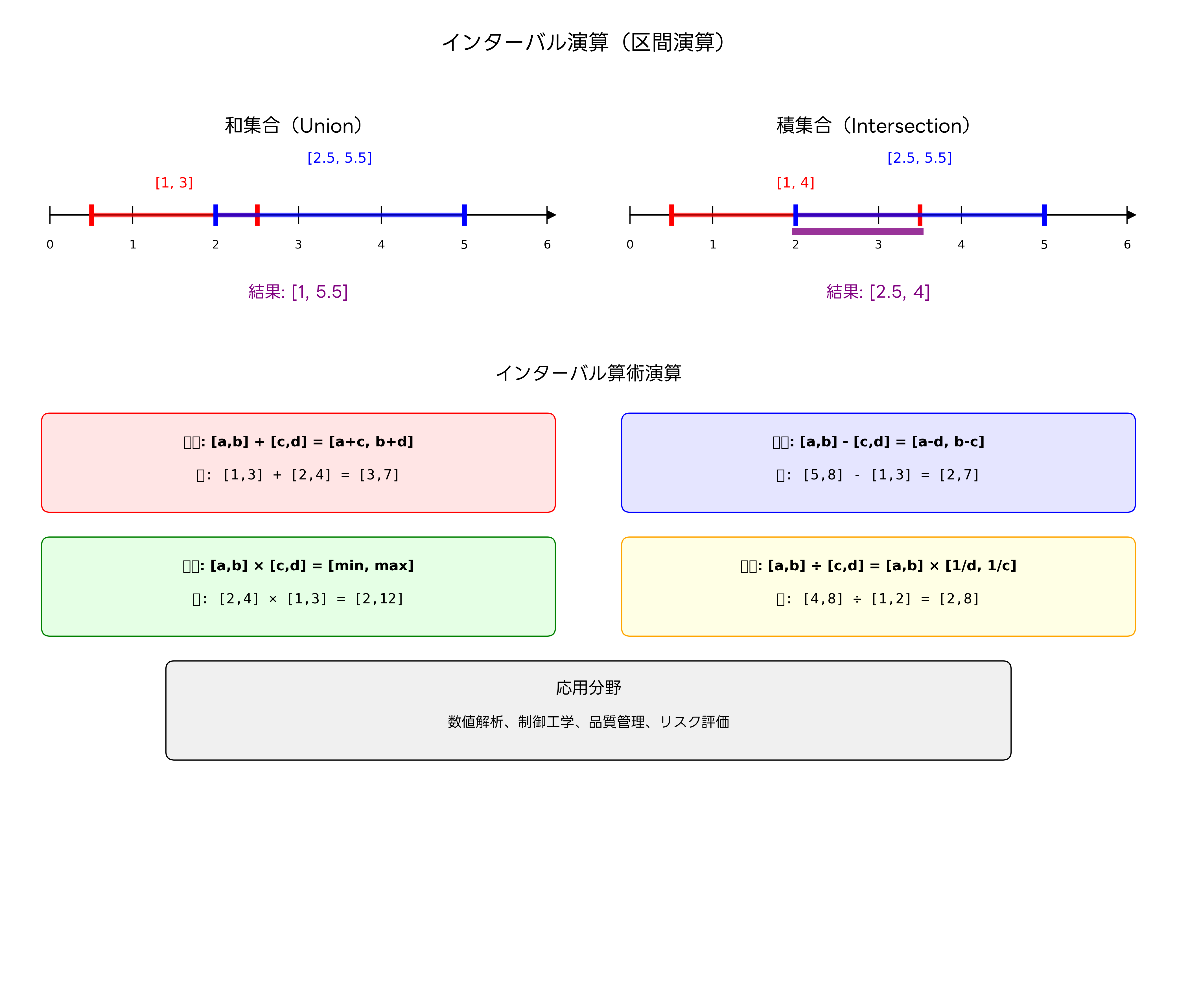
加算演算[a, b] + [c, d] = [a+c, b+d]は、各区間の最小値同士、最大値同士を加算します。例えば、[2, 5] + [1, 3] = [3, 8]となります。この演算は、測定値に誤差がある場合の合計値の範囲を求める際に使用されます。製造現場での部品寸法の公差計算や、品質管理システムでの累積誤差の評価に応用されています。
減算演算[a, b] - [c, d] = [a-d, b-c]では、被減数の最小値から減数の最大値を引き、被減数の最大値から減数の最小値を引きます。この操作により、差の取りうる範囲を正確に計算できます。例えば、[10, 15] - [2, 4] = [6, 13]となります。この演算は、在庫管理システムでの残量計算や、財務分析ソフトウェアでの収支差分析に活用されています。
乗算演算は最も複雑で、[a, b] × [c, d]を計算する際は、ac, ad, bc, bdの四つの値を計算し、その最小値と最大値を求めます。負の値を含む場合は特に注意が必要で、すべての組み合わせを検討する必要があります。この演算は、リスク分析や投資評価において、複数の不確実な要因の相互作用を評価する際に使用されます。
除算演算[a, b] ÷ [c, d]は、[a, b] × [1/d, 1/c]として定義されます。ただし、区間[c, d]に0が含まれる場合は特別な処理が必要です。この演算は、効率計算や比率分析において重要な役割を果たし、リスク管理ツールでの確率計算に応用されています。
インターバル演算の実装には、数値計算ライブラリや専用の計算ソフトウェアが利用されます。これらのツールは、丸め誤差の厳密な制御や効率的な演算アルゴリズムを提供し、高精度な区間計算を可能にします。
時間インターバルとスケジュール管理
時間インターバルは、時間的な区間や期間を表現する概念で、スケジュール管理、タスク管理、リソース配分などの分野で広く活用されています。この概念は、プロジェクト管理からリアルタイムシステムまで、時間を扱うあらゆるシステムの基盤となっています。
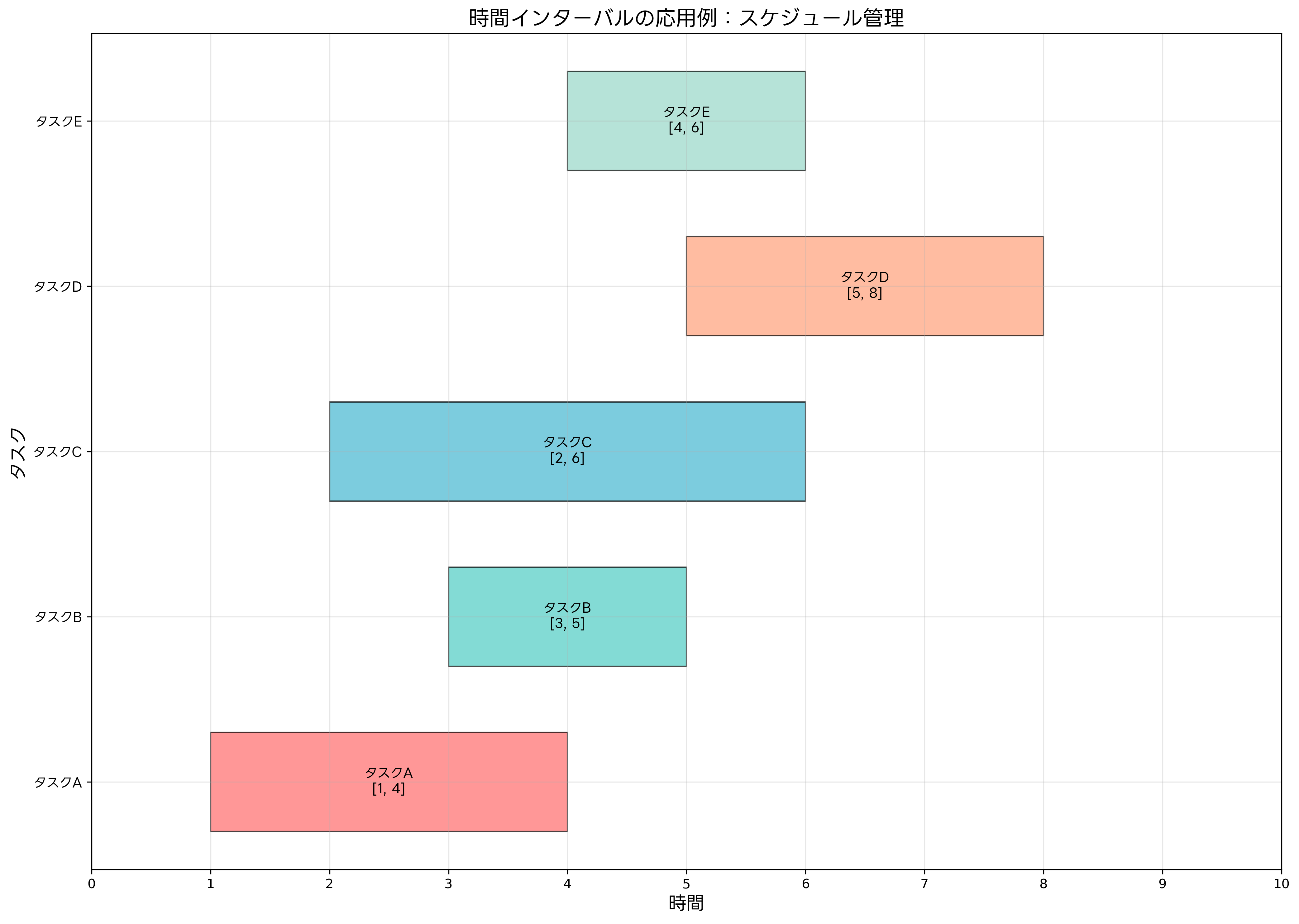
プロジェクト管理における時間インターバルは、各タスクの開始時刻と終了時刻によって定義されます。例えば、タスクAが[9:00, 12:00]の時間インターバルで実行される場合、このタスクは午前9時に開始し、正午に終了することを意味します。この表現により、複数のタスク間の時間的な関係を明確に把握でき、スケジュールの最適化が可能になります。
ガントチャートは、時間インターバルを視覚的に表現する代表的な手法です。各タスクの時間インターバルを横棒で表示し、プロジェクト全体の進行状況を一目で理解できます。現代のプロジェクト管理ソフトウェアは、このような時間インターバルの操作を効率化し、リソース配分の最適化や進捗管理の自動化を実現しています。
リアルタイムシステムでは、時間インターバルはタスクのデッドラインや実行周期を表現するために使用されます。例えば、制御システムにおいて、センサーデータの読み取りが[0ms, 10ms]の間隔で実行される必要がある場合、この時間インターバル内でタスクが完了することが求められます。リアルタイムOSや組み込みシステム開発ツールは、このような時間制約を満たすためのスケジューリング機能を提供しています。
時間インターバルの重複検出は、会議室予約システムや医療機関の予約システムなどで重要な機能です。二つの時間インターバル[a1, b1]と[a2, b2]が重複するかどうかは、max(a1, a2) < min(b1, b2)という条件で判定できます。この計算により、ダブルブッキングを防ぎ、効率的なリソース利用を実現できます。
カレンダーアプリケーションやスケジュール管理システムでは、時間インターバルの操作が中核機能となっています。定期的なイベントの生成、空き時間の検索、会議時間の調整など、様々な操作が時間インターバルの概念に基づいて実装されています。
インターバル木とデータ構造
インターバル木は、区間データを効率的に管理するための特殊なデータ構造です。この構造により、区間の検索、挿入、削除をO(log n)の時間計算量で実行でき、大量の区間データを扱うアプリケーションにおいて威力を発揮します。
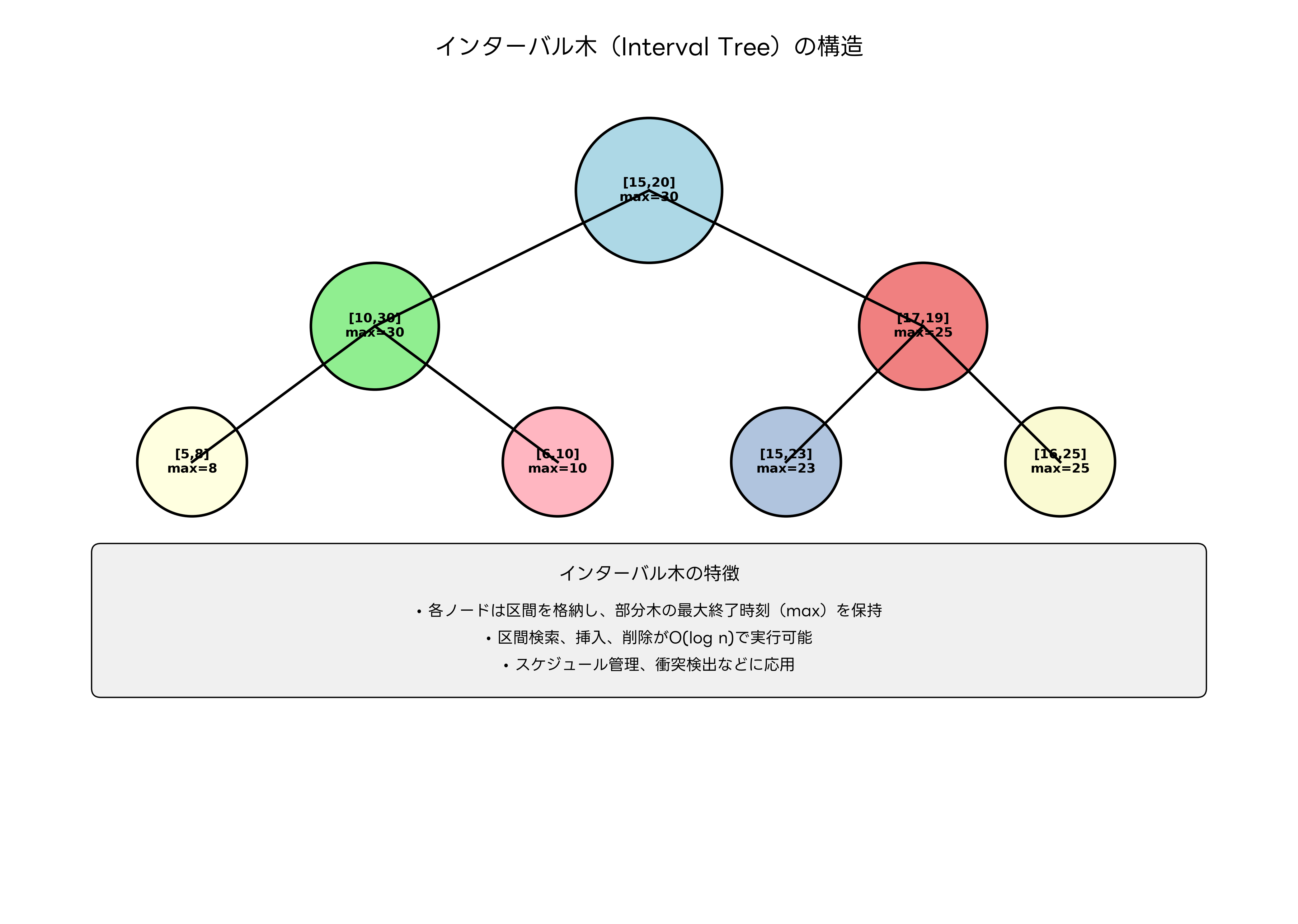
インターバル木の各ノードは、一つの区間と、その部分木に含まれる区間の最大終了時刻を保持します。この追加情報により、検索時に不要な部分木を効率的に枝刈りできます。例えば、区間[10, 20]を検索する際、あるノードの部分木の最大終了時刻が9である場合、その部分木には検索対象と重複する区間が存在しないことが確実にわかります。
区間検索アルゴリズムは、与えられた区間と重複するすべての区間を効率的に発見します。根ノードから開始し、各ノードで左の子ノードの最大終了時刻を確認し、検索対象の区間と重複する可能性がある方向に進むことで、効率的な検索を実現します。この手法により、全区間を線形探索する場合のO(n)に対し、O(log n + k)(kは結果の数)の時間計算量を達成できます。
インターバル木の実装には、データ構造アルゴリズムライブラリや専用のデータベースが利用されます。これらのツールは、メモリ効率の最適化やマルチスレッド対応など、実用的な機能を提供しています。
バランス型インターバル木では、AVL木や赤黒木の平衡化アルゴリズムを拡張し、区間の挿入や削除後も木の高さをO(log n)に保ちます。この平衡化により、最悪時でも効率的な操作が保証されます。平衡化の際は、各ノードの最大終了時刻も適切に更新する必要があり、実装の複雑さが増しますが、性能の安定性が向上します。
インターバル木は、遺伝子解析における配列アライメント、地理情報システムでの空間検索、音楽アプリケーションでの楽曲区間管理など、様々な分野で応用されています。特に、バイオインフォマティクスソフトウェアやGISシステムでは、インターバル木の効率性が重要な役割を果たしています。
統計学における信頼区間
統計学におけるインターバルの概念は、信頼区間として具現化されます。信頼区間は、母集団の真の値が含まれる可能性が高い範囲を示し、統計的推論の基盤となる重要な概念です。この概念により、標本データから母集団全体についての信頼性のある結論を導くことができます。
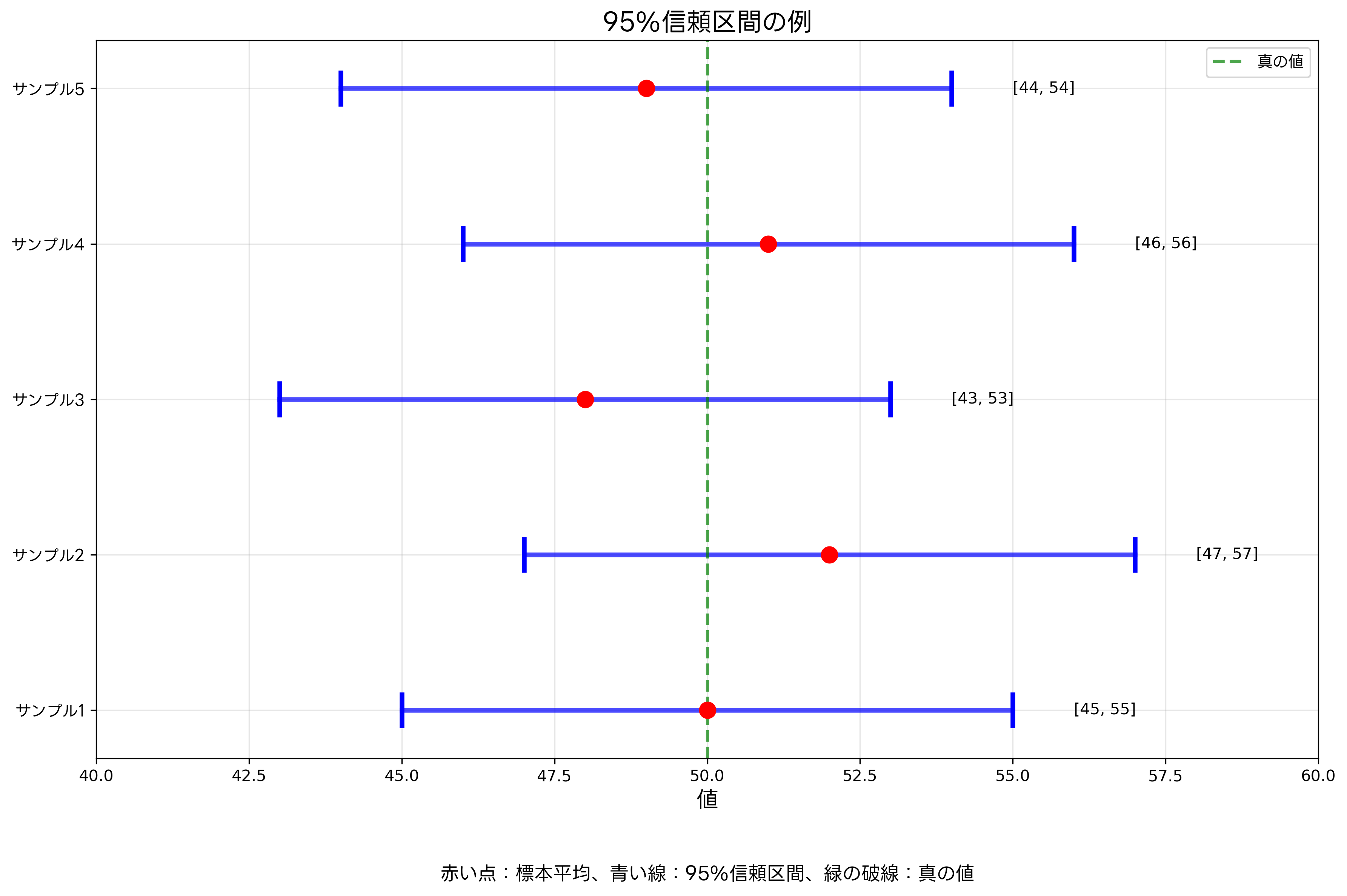
95%信頼区間は、統計学で最も一般的に使用される信頼水準です。これは、同じ方法で100回標本を取得し信頼区間を計算した場合、そのうち約95回は真の母集団平均を含む区間が得られることを意味します。例えば、製品の品質測定において、平均重量の95%信頼区間が[98.5g, 101.5g]である場合、真の平均重量がこの範囲内にある確信度が95%であることを示します。
信頼区間の幅は、標本サイズと標本の分散によって決まります。標本サイズが大きいほど、また分散が小さいほど、信頼区間は狭くなり、より精密な推定が可能になります。この関係性を理解することで、必要な精度を達成するための適切な標本サイズを事前に計算できます。統計解析ソフトウェアは、このような計算を自動化し、研究者や分析者の業務を効率化しています。
仮説検定における信頼区間の役割も重要です。帰無仮説で仮定された値が信頼区間に含まれない場合、その仮説を棄却する根拠となります。例えば、新薬の効果を検証する際、既存薬との効果差の95%信頼区間が[2.1, 5.8]である場合、効果差が0(効果なし)という帰無仮説を棄却できます。
ベイズ統計における信頼区間の概念は、信用区間として知られています。これは、与えられたデータに基づいて、真の値がある区間内にある確率を直接的に表現します。この手法は、機械学習ライブラリや予測分析ツールで広く採用され、不確実性を含む予測結果の解釈に活用されています。
品質管理における管理図では、信頼区間の概念を応用した管理限界線が使用されます。プロセスの測定値が信頼区間を外れた場合、プロセスに異常が発生した可能性を示唆し、適切な対応が必要となります。品質管理ソフトウェアは、このような異常検出を自動化し、製造品質の向上に貢献しています。
応用情報技術者試験での出題傾向
応用情報技術者試験において、インターバルの概念は様々な形で出題されます。特に、アルゴリズムとデータ構造、数値計算、システム管理の分野で頻繁に登場し、実務に直結した問題として重要な位置を占めています。
午前問題では、インターバル木の基本的な性質や操作の時間計算量に関する問題が出題されます。例えば、「n個の区間を格納するインターバル木において、ある区間と重複する区間を検索する際の時間計算量はどれか」といった問題形式が典型的です。この種の問題に対応するため、アルゴリズム参考書やデータ構造テキストを活用した理論の理解が重要です。
スケジュール管理に関する問題では、タスクの時間インターバルを基にした最適スケジューリングアルゴリズムが問われます。「最早開始時刻と最遅終了時刻が与えられた複数のタスクについて、すべてのタスクを実行可能なスケジュールを求める手法はどれか」といった実践的な問題が出題されます。これらの問題に対応するため、プロジェクト管理の教科書での学習が有効です。
午後問題では、より複合的な問題として、インターバルの概念を活用したシステム設計や性能分析が出題されます。例えば、「リアルタイムシステムにおいて、複数のタスクが与えられた制約下でスケジュール可能かどうかを判定するアルゴリズムを設計せよ」といった問題形式があります。
数値計算の分野では、インターバル演算を用いた誤差解析や精度保証計算に関する問題が出題されることがあります。特に、科学技術計算や制御システムの分野での応用を想定した問題が多く、実際の業務で遭遇する可能性の高い内容となっています。
試験対策としては、理論的な理解と実践的な応用の両方が重要です。応用情報技術者試験対策書で基礎理論を固めつつ、プログラミング演習書でアルゴリズムの実装練習を行うことが効果的です。
実世界での応用とケーススタディ
インターバルの概念は、現実世界の様々な分野で重要な役割を果たしています。金融工学におけるリスク管理から医療分野での診断支援まで、幅広い応用例を通じてその実用性を理解することができます。
金融分野では、株価や為替レートの変動範囲を予測するためにインターバル解析が使用されます。例えば、ある株式の明日の終値が[1000円, 1200円]の区間内にある確率が90%という予測により、投資戦略の意思決定を支援します。金融データ分析ツールやリスク管理システムは、このようなインターバル計算を高速に実行し、トレーダーやファンドマネージャーの判断を支援しています。
製造業における品質管理では、製品の仕様範囲をインターバルで表現し、製造プロセスの管理に活用します。例えば、自動車部品の寸法が[99.8mm, 100.2mm]の範囲内にある必要がある場合、製造装置の設定や検査基準をこの範囲に基づいて決定します。製造実行システムや品質検査装置は、このような仕様管理を自動化し、品質向上と効率化を同時に実現しています。
医療分野では、診断における正常値の範囲や薬物の有効濃度範囲をインターバルで表現します。例えば、血糖値の正常範囲が[70mg/dL, 100mg/dL]である場合、この範囲を外れた測定値は糖尿病などの疾患の指標となります。医療情報システムや診断支援ソフトウェアは、このような基準値管理を通じて医療従事者の判断を支援しています。
交通制御システムでは、信号機のタイミング制御や交通流量の最適化にインターバルの概念が応用されます。各信号の青時間を[30秒, 60秒]の範囲で動的に調整することで、交通状況に応じた最適な制御を実現します。交通管理システムやIoT交通センサーは、リアルタイムデータに基づいてこのような制御を自動化しています。
環境監視システムでは、大気汚染物質の濃度や温度、湿度などの環境指標の許容範囲をインターバルで定義します。例えば、PM2.5の濃度が[0μg/m³, 35μg/m³]の範囲を超えた場合に警報を発するシステムが構築されています。環境モニタリングシステムや大気質センサーは、このような監視機能を提供し、環境保護に貢献しています。
まとめ
インターバルの概念は、数学的な基礎理論から実用的な応用まで、情報技術の様々な分野にわたって重要な役割を果たしています。区間演算による数値計算の精度保証、時間インターバルによるスケジュール管理の効率化、インターバル木による高速データ検索、統計学における信頼区間の活用など、その応用範囲は極めて広範です。
現代のデジタル社会において、不確実性や範囲を含むデータの処理はますます重要になっています。IoTデバイスから収集される大量のセンサーデータ、金融市場の変動予測、製造プロセスの品質管理など、あらゆる場面でインターバルの概念が活用されています。データ分析プラットフォームやクラウド計算サービスは、このような高度な計算を大規模に実行する基盤を提供しています。
応用情報技術者試験の観点からも、インターバルの理解は必須の知識です。アルゴリズムの時間計算量、データ構造の効率性、システムの性能評価など、試験で問われる多くのトピックがインターバルの概念と密接に関連しています。理論的な理解と実践的な応用能力の両方を身につけることで、試験合格だけでなく、実務での問題解決能力も向上します。
技術の進歩とともに、インターバルの概念はさらに重要性を増しています。人工知能における不確実性の表現、量子コンピューティングでの確率的計算、分散システムでの一貫性保証など、最先端の技術分野でもインターバルの概念が活用されています。継続的な学習と実践により、この重要な概念を深く理解し、将来の技術革新に貢献する能力を身につけることができるでしょう。