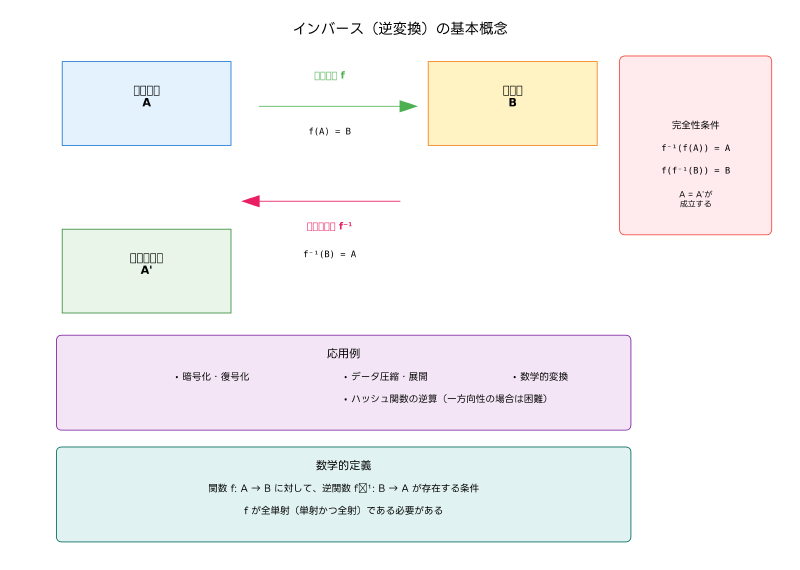
情報技術の世界において、インバース(逆変換)は極めて重要な概念です。データの変換と復元、暗号化と復号化、圧縮と展開など、様々な場面でインバース操作が活用されています。応用情報技術者試験においても、数学的な基礎から実用的な応用まで幅広く出題される重要なトピックです。
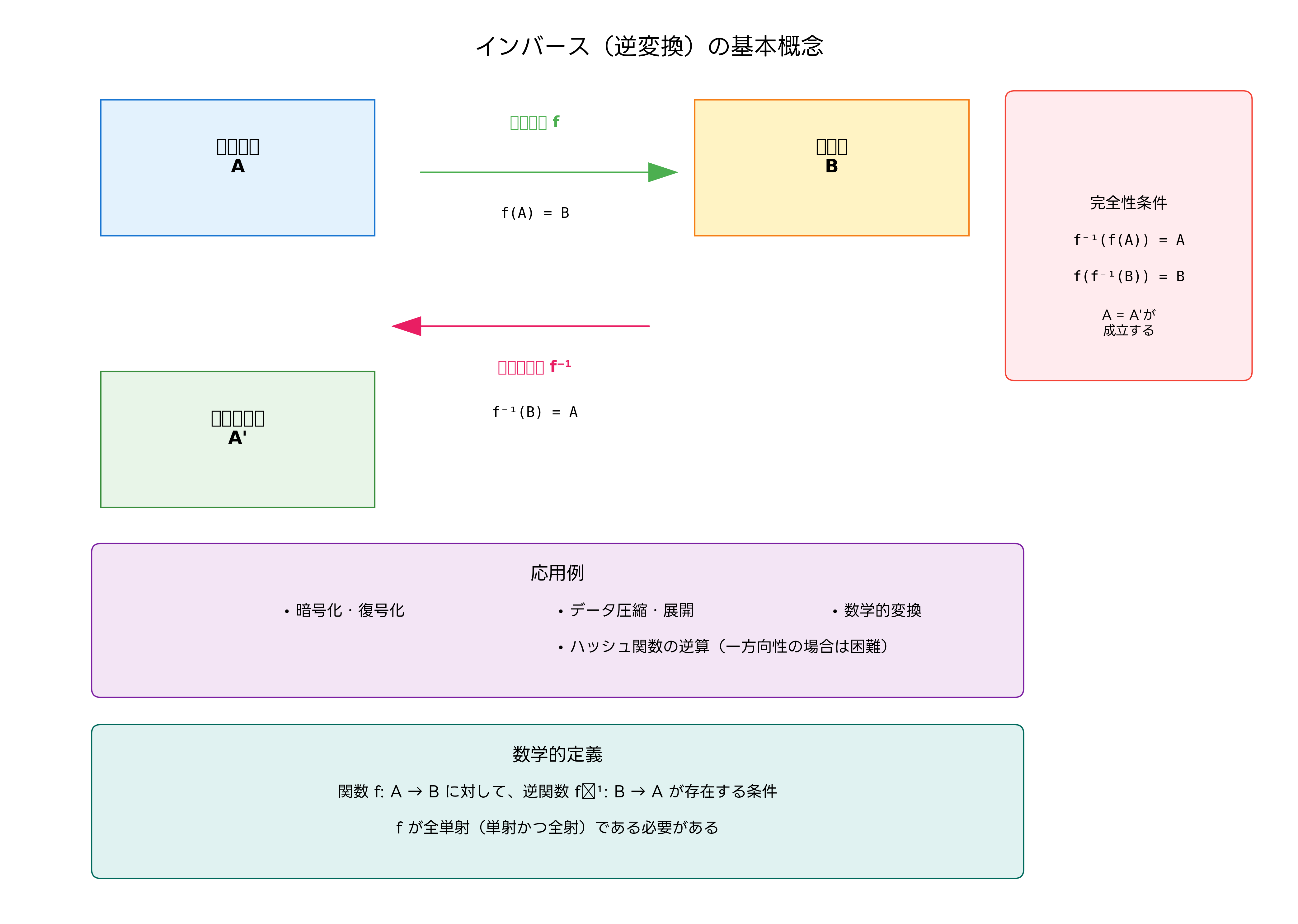
インバースとは、ある変換操作に対して、その効果を打ち消し、元の状態に戻すための逆操作のことを指します。数学的には、関数fに対してf⁻¹が逆関数であり、f⁻¹(f(x)) = xおよびf(f⁻¹(y)) = yが成立します。この概念は情報処理の多くの分野で応用され、現代のデジタル社会を支える基盤技術となっています。
インバースの数学的基礎
インバースの理解には、まず数学的な基礎を把握することが重要です。関数の逆関数が存在するためには、その関数が全単射(単射かつ全射)である必要があります。単射とは、異なる入力値に対して異なる出力値が対応することを意味し、全射とは、出力の範囲のすべての値に対して入力値が存在することを意味します。
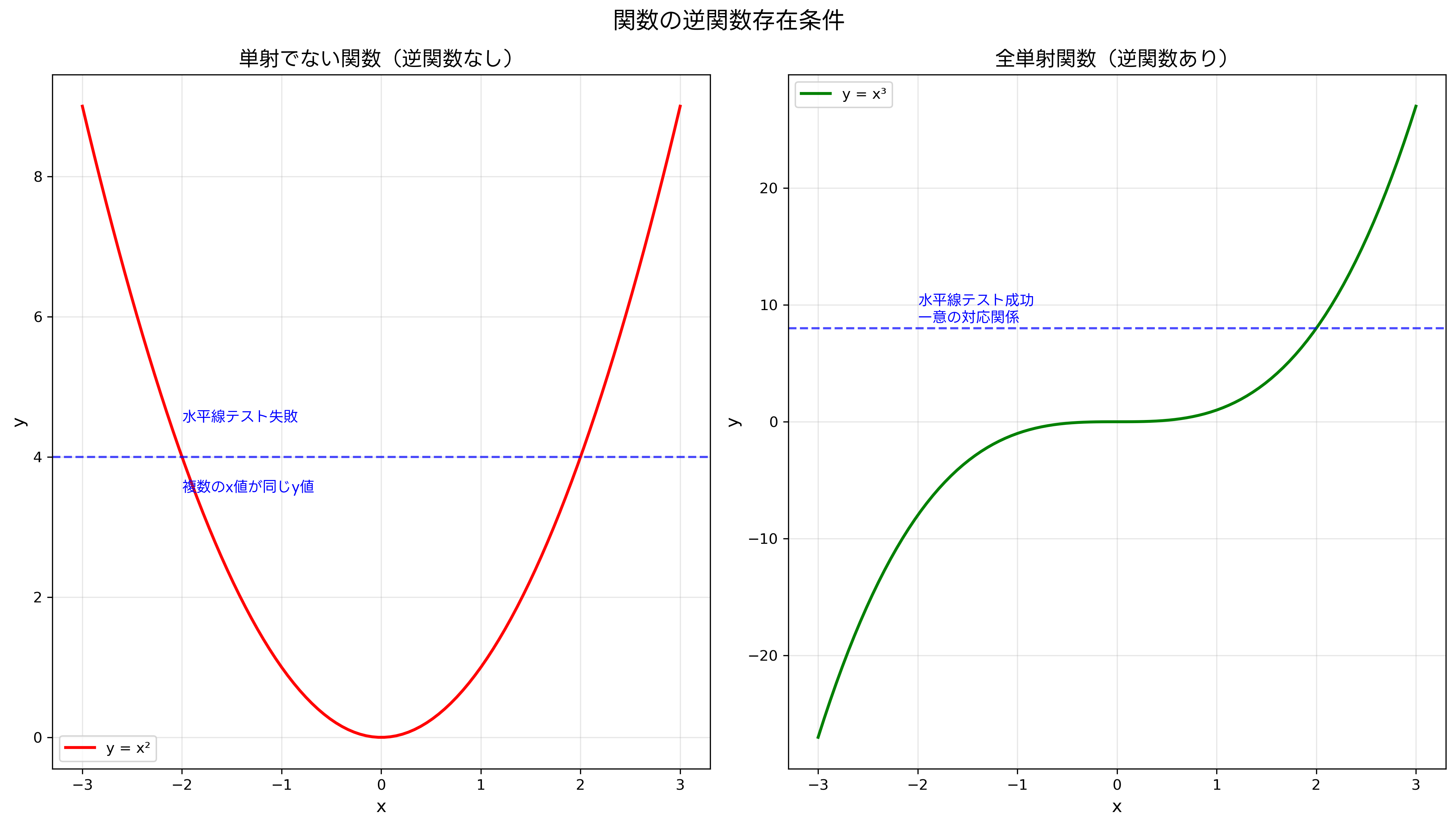
この条件を満たさない関数では、完全な逆変換は不可能です。例えば、y = x²のような関数は、負の数に対しても正の数に対しても同じ出力を生成するため、逆関数は一意に決定できません。このような場合、定義域を制限することで逆関数を定義することが可能になります。
実際の応用では、完全な逆変換が困難な場合でも、近似的な逆変換や部分的な逆変換が有用です。数学計算ソフトウェアを使用することで、複雑な逆関数の計算や可視化が容易になります。
行列のインバース(逆行列)
線形代数において、行列のインバースは特別に重要な概念です。正方行列Aに対して、その逆行列A⁻¹は、A × A⁻¹ = A⁻¹ × A = I(単位行列)を満たす行列です。逆行列の存在は、行列の行列式(determinant)が0でないことと等価です。
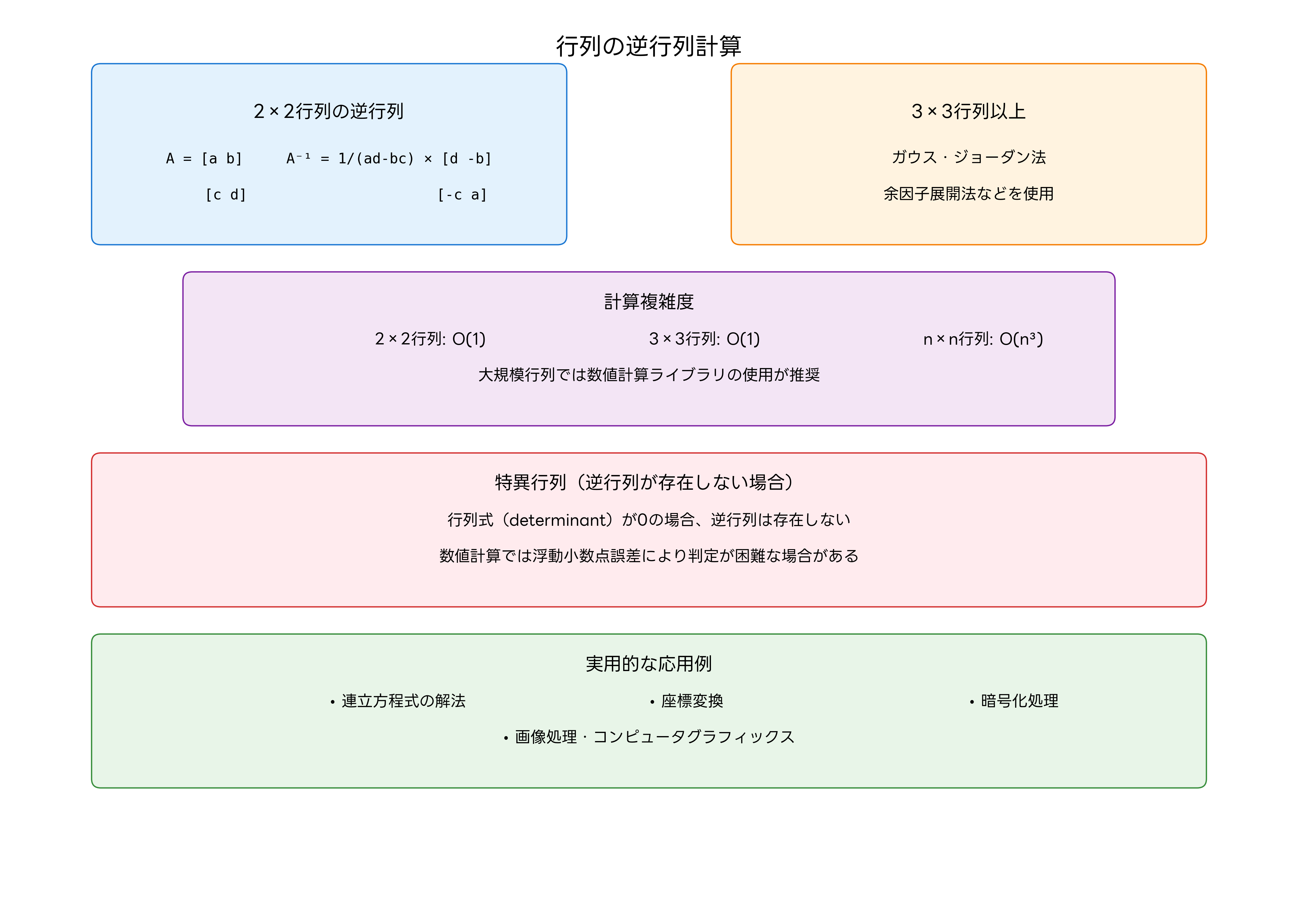
2×2行列の逆行列は比較的簡単に求めることができますが、大きな行列の逆行列計算は計算量が大きく、数値的な安定性も考慮する必要があります。実際の計算では、高性能な数値計算ライブラリや行列計算専用ソフトウェアを活用することが一般的です。
逆行列は連立方程式の解法において中心的な役割を果たします。Ax = bという形の連立方程式は、Aの逆行列が存在する場合、x = A⁻¹bとして解くことができます。この性質は、工学や科学計算の多くの分野で活用されています。
暗号化・復号化におけるインバース
情報セキュリティの分野では、インバースの概念が暗号化と復号化の基盤となっています。対称暗号では、同一の鍵を使用して暗号化と復号化を行い、公開鍵暗号では、数学的に関連する公開鍵と秘密鍵のペアを使用します。
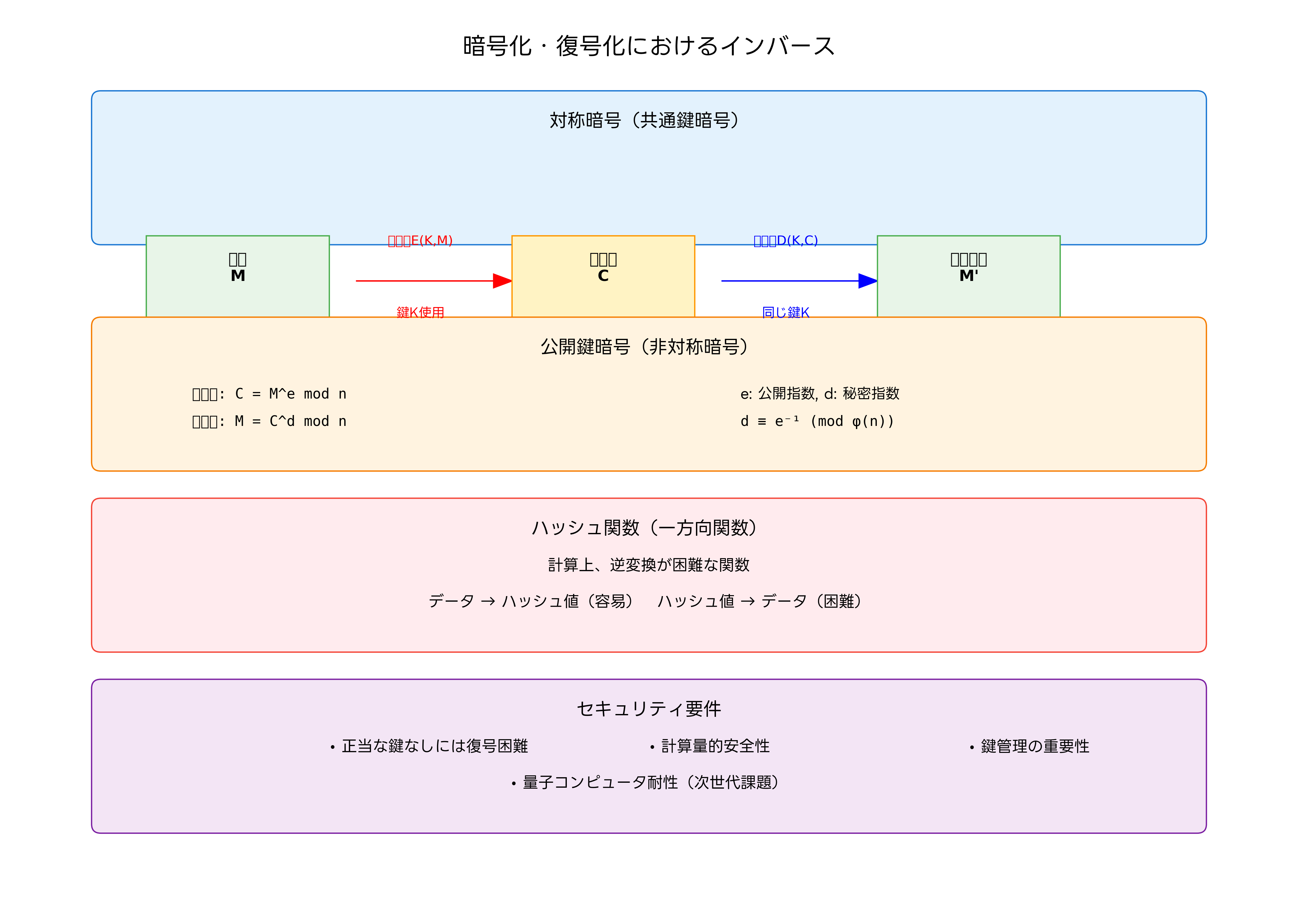
RSA暗号は、大きな整数の素因数分解の困難性に基づいた公開鍵暗号システムです。暗号化はC = M^e mod nで表され、復号化はM = C^d mod nで行われます。ここで、eとdは数学的に関連した指数であり、d ≡ e⁻¹ (mod φ(n))の関係があります。この数学的な関係性により、暗号化と復号化の相互変換が保証されます。
現代の暗号システムを実装する際には、暗号化ライブラリやセキュリティ開発ツールの活用が重要です。また、量子コンピュータの発展により、従来の暗号方式の安全性に関する議論も活発化しており、量子暗号関連書籍による最新動向の把握も必要です。
ハッシュ関数は、一方向関数として設計されており、計算上の逆変換は困難です。MD5、SHA-256などのハッシュ関数は、入力データから固定長のハッシュ値を生成しますが、そのハッシュ値から元のデータを復元することは実質的に不可能です。この性質により、パスワードの安全な保存やデジタル署名の実現が可能になります。
データ圧縮・展開でのインバース
データ圧縮技術では、原理的に可逆圧縮と非可逆圧縮の2つのアプローチがあります。可逆圧縮では、圧縮されたデータから完全に元のデータを復元できますが、非可逆圧縮では、一部の情報が失われるため完全な復元は不可能です。
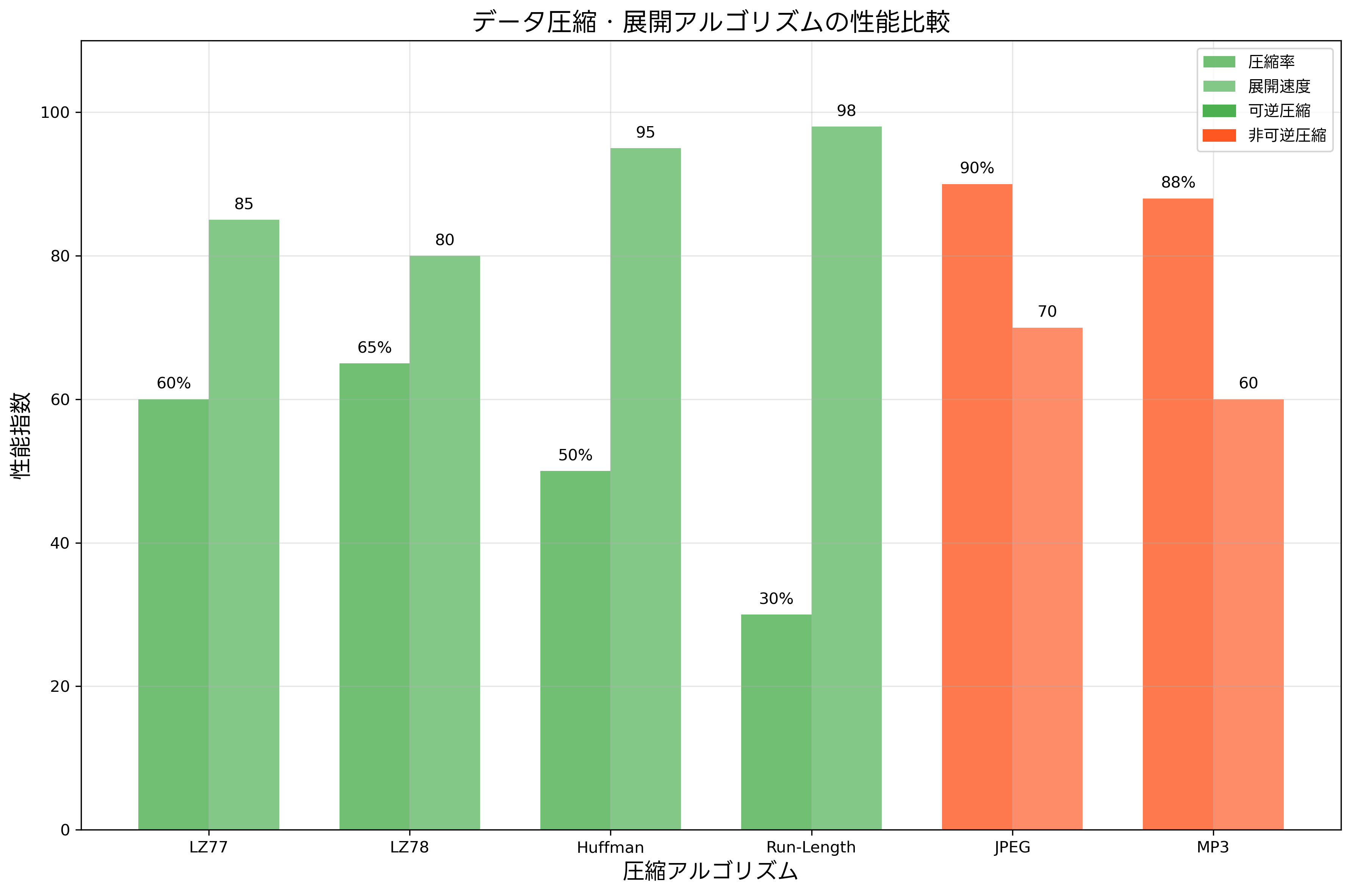
LZ77、LZ78、Huffman符号化などの可逆圧縮アルゴリズムは、データの統計的特性や反復パターンを利用してデータサイズを削減し、展開時には完全に元のデータを復元します。これらのアルゴリズムは、テキストファイルやプログラムファイルなど、データの完全性が重要な場合に使用されます。
一方、JPEG画像圧縮やMP3音声圧縮などの非可逆圧縮では、人間の知覚特性を考慮して重要でない情報を削除することで高い圧縮率を実現します。これらの技術では、完全な逆変換は不可能ですが、実用上十分な品質での復元が可能です。
現代のデータ処理において、効率的な圧縮・展開処理を実現するためには、高性能圧縮ソフトウェアやデータ圧縮ライブラリの活用が重要です。特に、大容量データを扱う企業では、エンタープライズ向け圧縮ソリューションの導入により、ストレージコストの削減と処理効率の向上を実現できます。
信号処理におけるインバース変換
信号処理の分野では、フーリエ変換とその逆変換が中心的な役割を果たしています。フーリエ変換は時間領域の信号を周波数領域に変換し、逆フーリエ変換により周波数領域から時間領域への復元が可能です。この変換ペアにより、信号のスペクトル解析やフィルタリング処理が実現されます。
離散フーリエ変換(DFT)とその高速実装であるFFT(Fast Fourier Transform)は、デジタル信号処理の基礎技術です。音声処理、画像処理、通信システムなど、様々な分野でFFTとその逆変換(IFFT)が活用されています。これらの技術を効果的に活用するためには、信号処理ソフトウェアやFFT専用ハードウェアの理解が重要です。
ウェーブレット変換も重要なインバース変換の例です。ウェーブレット変換では、基底となるウェーブレット関数を用いて信号を多解像度解析し、その逆変換により元の信号を復元します。この技術は、画像圧縮(JPEG2000)、ノイズ除去、特徴抽出などの用途で広く使用されています。
機械学習におけるインバース問題
機械学習の分野では、順問題(モデルからデータを生成)に対する逆問題(データからモデルやパラメータを推定)が重要な課題となっています。特に、深層学習における生成モデルでは、潜在空間から観測データへの変換とその逆変換が研究の中心テーマです。
変分オートエンコーダー(VAE)や生成敵対ネットワーク(GAN)などの生成モデルでは、エンコーダとデコーダの組み合わせにより、データの圧縮表現と復元を学習します。これらのモデルでは、完全な逆変換ではなく、確率的または近似的な逆変換を扱います。
機械学習モデルの開発と評価には、深層学習フレームワークやGPU計算環境が不可欠です。また、理論的な理解を深めるためには、機械学習数学教科書の学習も重要です。
応用情報技術者試験での出題傾向
応用情報技術者試験では、インバースに関する問題が数学的基礎から実用的応用まで幅広く出題されます。特に、線形代数における逆行列の計算、暗号化システムの理論、データ圧縮アルゴリズムの特性などが頻出テーマです。
午前問題では、逆行列の存在条件、行列式の計算、基本的な暗号化・復号化の仕組みなどが問われます。また、フーリエ変換の性質や信号処理における逆変換の応用についても出題されることがあります。これらの問題に対応するためには、応用情報技術者試験対策書や数学基礎参考書による学習が効果的です。
午後問題では、より実践的な文脈でのインバース操作の理解が求められます。暗号システムの設計、データベースの正規化と非正規化、アルゴリズムの時間計算量と空間計算量のトレードオフなど、システム設計における逆変換の考慮が重要です。
数値計算における課題と対策
実際の数値計算においては、理論的に完全なインバースが存在する場合でも、浮動小数点演算の精度制限により完全な逆変換が困難な場合があります。特に、条件数の大きな行列の逆行列計算では、数値的不安定性が問題となります。
条件数とは、入力の小さな変化が出力にどの程度影響するかを示す指標です。条件数が大きい行列では、わずかな入力誤差が大きな出力誤差を引き起こす可能性があります。このような問題に対処するため、特異値分解(SVD)や疑似逆行列などの数値安定な手法が開発されています。
実用的な数値計算システムの構築には、高精度数値計算ライブラリや数値解析専門書の活用が重要です。また、計算精度と処理速度のバランスを考慮した実装が求められます。
最新技術動向とインバース
近年の人工知能と量子コンピューティングの発展により、インバース問題に対する新しいアプローチが注目されています。量子アルゴリズムでは、従来のコンピュータでは困難だった大規模な逆行列計算や最適化問題の効率的な解法が期待されています。
機械学習における物理情報ニューラルネットワーク(PINN)では、物理法則を制約として組み込むことで、逆問題の解の精度と安定性を向上させています。この技術は、医療画像診断、材料科学、気象予測などの分野で実用化が進んでいます。
これらの最新技術に関する情報収集には、量子コンピューティング関連書籍やAI技術動向レポートが有用です。また、実践的なスキル習得のためには、プログラミング演習環境での手を動かした学習が重要です。
実装上の考慮事項とベストプラクティス
インバース操作を実装する際には、計算効率、数値安定性、メモリ使用量などの多面的な考慮が必要です。特に、大規模なデータセットや高次元の問題では、アルゴリズムの選択と実装の最適化が重要になります。
メモリ効率の観点では、インプレース計算やスパース行列の活用により、メモリ使用量を削減できます。また、並列処理や分散処理により、計算時間の短縮が可能です。これらの最適化技術の実装には、並列処理ライブラリや高性能コンピューティング参考書の理解が有用です。
エラーハンドリングも重要な考慮事項です。逆変換が存在しない場合や数値的に不安定な場合の適切な処理により、システム全体の堅牢性を確保できます。また、計算精度の監視と動的な精度調整により、品質と性能のバランスを最適化できます。
まとめ
インバース(逆変換)は、現代の情報技術において基盤的な概念であり、数学的理論から実用的応用まで幅広い知識が求められます。暗号化・復号化、データ圧縮・展開、信号処理、機械学習など、様々な分野でインバース操作が活用されており、その理解は情報技術者にとって不可欠です。
応用情報技術者試験においても、インバースに関する問題は重要な出題テーマであり、数学的基礎から実装技術まで包括的な理解が求められます。継続的な学習と実践により、理論と応用の両面でのスキル向上を図ることが重要です。
技術の進歩とともに、インバース問題に対する新しい解法や応用分野も拡大しています。最新の技術動向を把握し、基礎理論と実践技術の両面でスキルを磨くことで、変化する技術環境に対応できる能力を身につけることができます。効果的な学習のためには、総合的な技術書籍による理論学習と、実践的な開発環境での演習を組み合わせることが推奨されます。