回帰分析は、統計学と機械学習の分野において最も重要で基本的な解析手法の一つです。変数間の関係性を数学的にモデル化し、予測や因果関係の分析を行うこの手法は、ビジネス、科学研究、政策決定など幅広い分野で活用されています。応用情報技術者試験においても頻出の重要トピックであり、データサイエンスやAI技術の理解において欠かせない基礎知識です。
回帰分析の本質は、一つまたは複数の説明変数(独立変数)を使用して、目的変数(従属変数)の値を予測することにあります。この手法により、データに隠れているパターンや関係性を発見し、将来の値を予測したり、変数間の影響を定量化したりすることが可能になります。
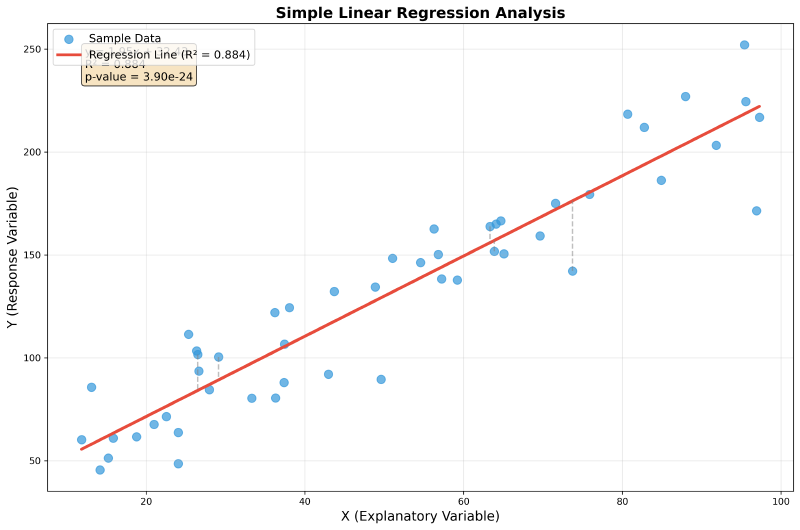
単純回帰分析:基本的な関係性の発見
単純回帰分析は、一つの説明変数と一つの目的変数の間の線形関係をモデル化する最も基本的な回帰分析手法です。数学的には、y = ax + b という直線の方程式で表現され、この直線がデータポイントに最も適合するように係数aとbを決定します。
この手法では、最小二乗法という統計的手法を用いて最適な回帰直線を求めます。最小二乗法は、実際の観測値と回帰直線による予測値の差の二乗和を最小化することで、最も適合度の高い直線を見つける方法です。現代では、統計解析ソフトウェアを使用することで、複雑な計算を自動化し、効率的に分析を行うことができます。
単純回帰分析の実装には、適切なデータ分析用ノートパソコンや高性能ワークステーションが必要です。特に大規模なデータセットを扱う場合は、十分な処理能力とメモリ容量が重要になります。
回帰直線の傾きは説明変数が目的変数に与える影響の大きさを表し、切片は説明変数がゼロの時の目的変数の期待値を表します。例えば、広告費と売上の関係を分析する場合、傾きは広告費を1単位増やすことで売上がどれだけ増加するかを示し、切片は広告費をかけない場合の基本的な売上を表します。
単純回帰分析では、決定係数(R²)という指標を用いてモデルの適合度を評価します。R²は0から1の値を取り、1に近いほど説明変数が目的変数の変動をよく説明していることを意味します。一般的に、R²が0.7以上であれば強い相関関係があると判断されますが、分野や用途によって基準は異なります。
実際の分析では、回帰分析の前提条件を満たしているかどうかの確認が重要です。線形性、独立性、等分散性、正規性という4つの前提条件が満たされていない場合、分析結果の信頼性が低下する可能性があります。これらの前提条件の検証には、統計検定用の専門書や回帰分析の実践ガイドが参考になります。
重回帰分析:複雑な関係性のモデル化
重回帰分析は、複数の説明変数を用いて目的変数を予測する高度な統計手法です。現実の現象は通常、複数の要因によって影響を受けるため、重回帰分析はより実用的で精度の高い分析を可能にします。数学的には、y = a₁x₁ + a₂x₂ + … + aₙxₙ + b という多変数の線形方程式で表現されます。

重回帰分析では、各説明変数の偏回帰係数が重要な意味を持ちます。偏回帰係数は、他の説明変数を一定に保った状態で、その変数が1単位変化したときの目的変数の変化量を表します。これにより、複数の要因の中から最も影響力の大きい要因を特定したり、各要因の独立した効果を定量化したりすることができます。
多重共線性は重回帰分析において注意すべき重要な問題です。説明変数同士が強い相関関係にある場合、回帰係数の推定が不安定になり、解釈が困難になります。多重共線性の診断には、VIF(分散拡大要因)やCondition Indexなどの指標を用います。これらの問題を解決するため、多重共線性診断ツールや高度な統計ソフトウェアの導入が推奨されます。
変数選択は重回帰分析における重要なプロセスです。ステップワイズ法、前進選択法、後退除去法などの手法を用いて、最適な説明変数の組み合わせを見つけます。AIC(赤池情報量規準)やBIC(ベイズ情報量規準)などの情報量規準を使用して、モデルの複雑さと適合度のバランスを考慮した最適なモデルを選択します。
重回帰分析の実装には、PythonのScikit-learnやRの統計パッケージなどが広く使用されています。これらのツールを効果的に活用するため、データサイエンス用プログラミング書籍や統計解析R入門書での学習が有効です。
回帰分析の種類と特徴
回帰分析には、データの性質や分析目的に応じて様々な種類があります。それぞれの手法には固有の特徴と適用場面があり、適切な手法を選択することが正確な分析結果を得るために重要です。
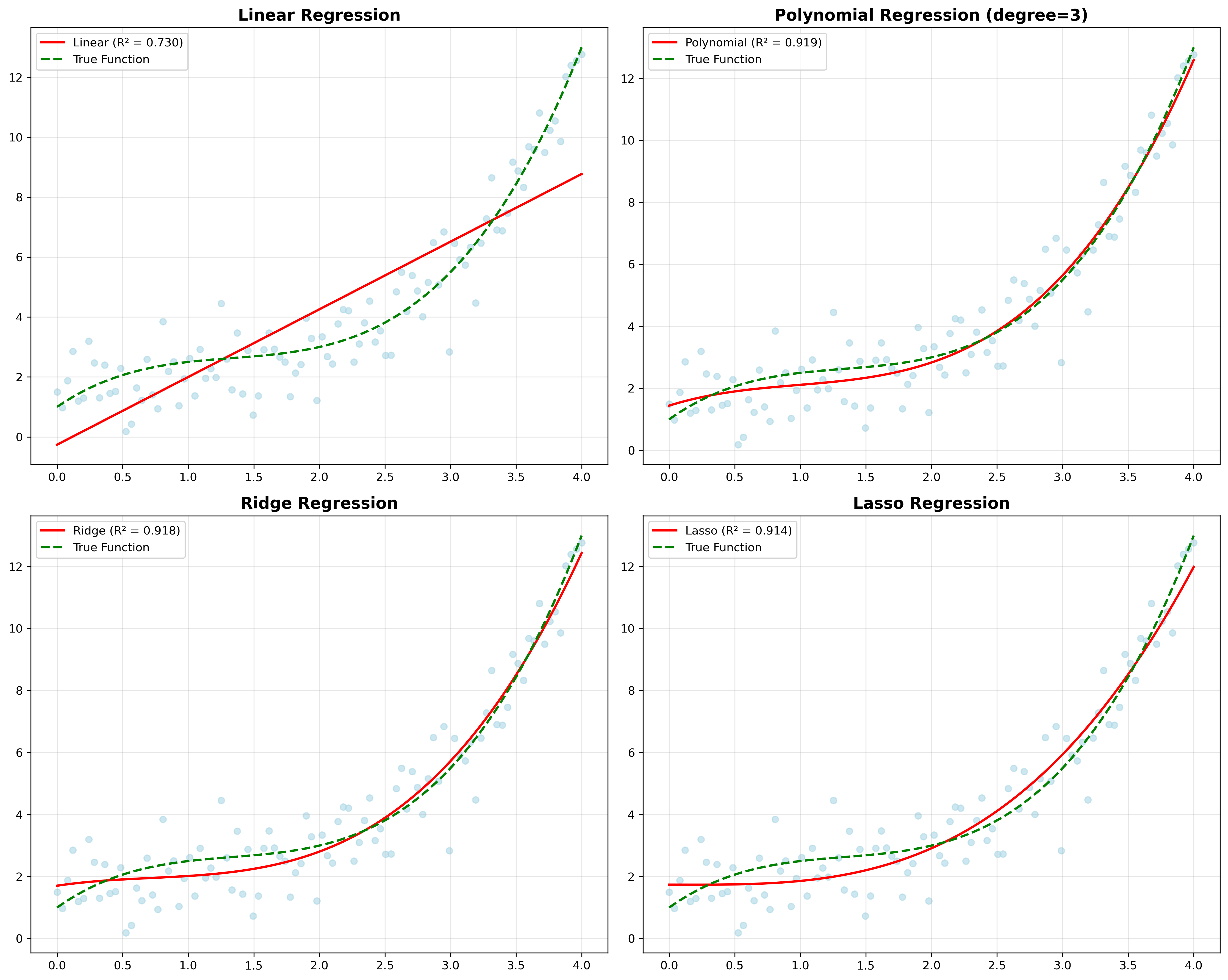
多項式回帰は、線形回帰を拡張して非線形の関係をモデル化する手法です。説明変数の高次項(x², x³など)を追加することで、曲線的な関係を表現できます。ただし、次数を高くしすぎると過学習の問題が生じる可能性があるため、適切な次数の選択が重要です。多項式回帰の実装と検証には、機械学習アルゴリズム解説書が参考になります。
リッジ回帰(Ridge Regression)は、正則化項を追加することで過学習を防ぐ手法です。回帰係数の二乗和にペナルティを課すことで、係数の値を小さく抑え、モデルの汎化性能を向上させます。特に説明変数の数が多い場合や多重共線性がある場合に有効です。
ラッソ回帰(Lasso Regression)は、L1正則化を用いる手法で、回帰係数の絶対値の和にペナルティを課します。この手法の特徴は、重要でない変数の係数を自動的にゼロにする変数選択機能を持つことです。これにより、解釈しやすいシンプルなモデルを構築できます。
エラスティックネット回帰は、リッジ回帰とラッソ回帰の特徴を組み合わせた手法です。L1正則化とL2正則化の両方を使用することで、それぞれの利点を活用できます。相関の高い変数群から代表的な変数を選択する場合などに特に有効です。
ロバスト回帰は、外れ値に対して頑健な推定を行う手法です。通常の最小二乗法は外れ値の影響を大きく受けますが、ロバスト回帰では外れ値の影響を抑制する損失関数を使用します。データに外れ値が多く含まれる場合や、測定誤差が大きい場合に有効です。
ベイズ回帰は、ベイズ統計学の枠組みで回帰分析を行う手法です。パラメータを確率分布として扱い、事前知識を組み込むことができます。不確実性の定量化や小標本での推定に優れており、医療や金融などの分野で活用されています。ベイズ回帰の理解には、ベイズ統計学入門書が有用です。
残差分析:モデルの妥当性の検証
残差分析は、回帰分析の結果が適切であるかを評価するための重要な手法です。残差とは、実際の観測値と回帰モデルによる予測値の差のことで、モデルが捉えきれていない部分を表します。残差の分析により、モデルの前提条件が満たされているか、改善すべき点があるかを判断できます。
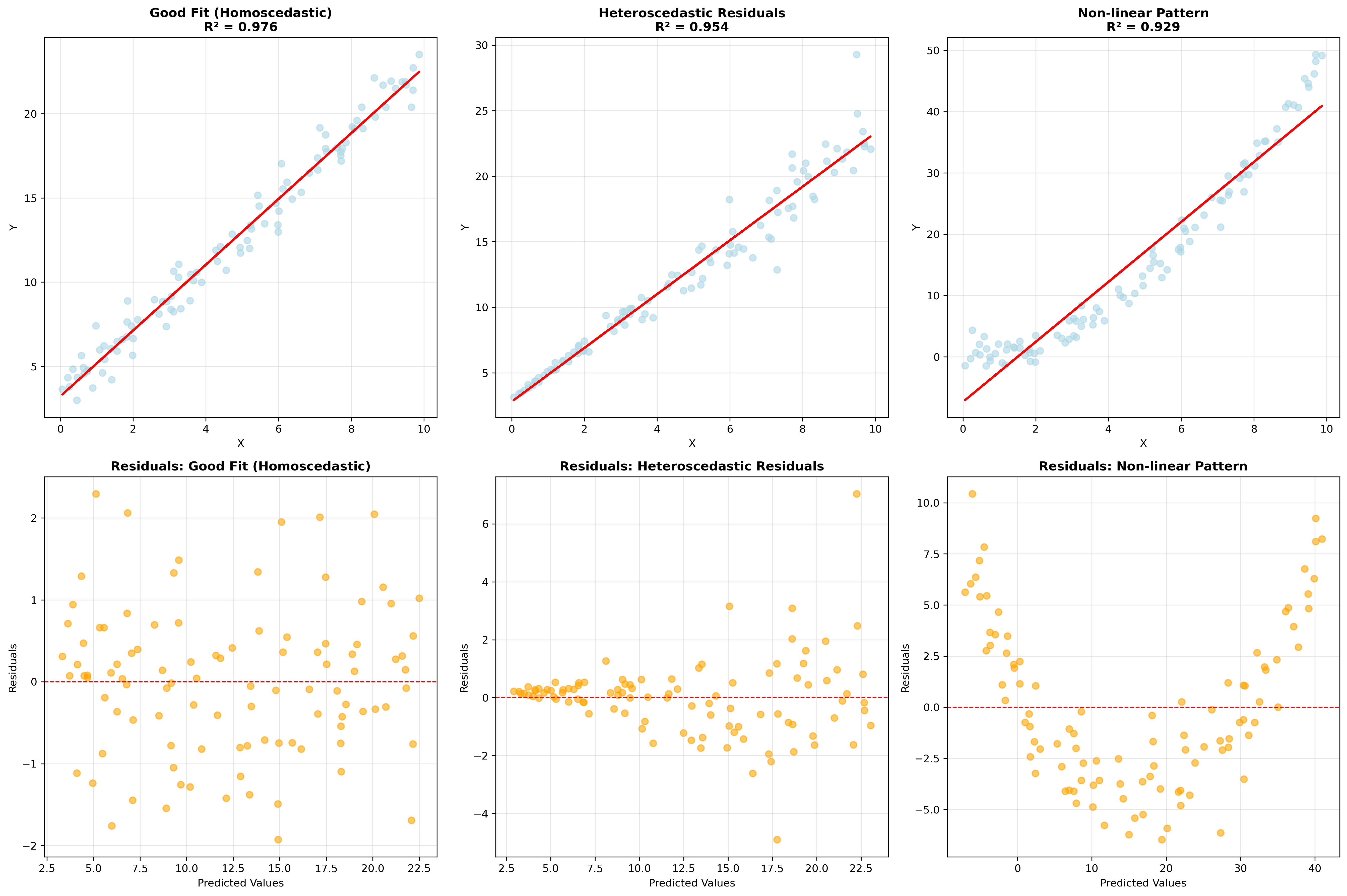
残差プロットは残差分析の基本的なツールです。横軸に予測値、縦軸に残差を取ったグラフを作成し、残差のパターンを視覚的に確認します。理想的な回帰モデルでは、残差がゼロの周りにランダムに散らばります。特定のパターンが見られる場合は、モデルに問題がある可能性があります。
不等分散性(ヘテロスケダスティシティ)は、残差の分散が予測値に応じて変化する問題です。残差プロットで残差の散らばりが予測値とともに変化する場合、この問題が疑われます。不等分散性がある場合は、重み付き最小二乗法や変数変換などの対処法を検討します。
系列相関(自己相関)は、時系列データにおいて残差が時間的に相関を持つ問題です。ダービン・ワトソン統計量やLjung-Box検定を用いて検出できます。系列相関がある場合は、自己回帰項の追加や差分の取得などの対処が必要です。これらの高度な分析には、時系列解析専門書が参考になります。
正規性の検定は、残差が正規分布に従うかを確認する手法です。Shapiro-Wilk検定やAnderson-Darling検定などを用いて統計的に検定できます。正規性が満たされない場合は、変数変換やロバスト回帰の使用を検討します。
外れ値の検出と処理も残差分析の重要な要素です。標準化残差やスチューデント化残差を用いて外れ値を特定し、データの確認や除外を検討します。外れ値の処理には慎重な判断が必要で、統計的外れ値検出手法に関する専門知識が重要です。
影響力の大きい観測値(レバレッジポイント)の検出も重要です。Cook距離やDFFITSなどの統計量を用いて、個々の観測値がモデル全体に与える影響を評価します。影響力の大きい観測値が見つかった場合は、データの妥当性を確認し、必要に応じてモデルの修正を行います。
モデル評価指標:精度と性能の測定
回帰分析の性能を評価するには、様々な指標を用いてモデルの精度を定量化します。これらの指標は、モデルの選択、改善、比較において重要な役割を果たします。適切な評価指標の選択は、分析の目的や使用するデータの特性によって決まります。
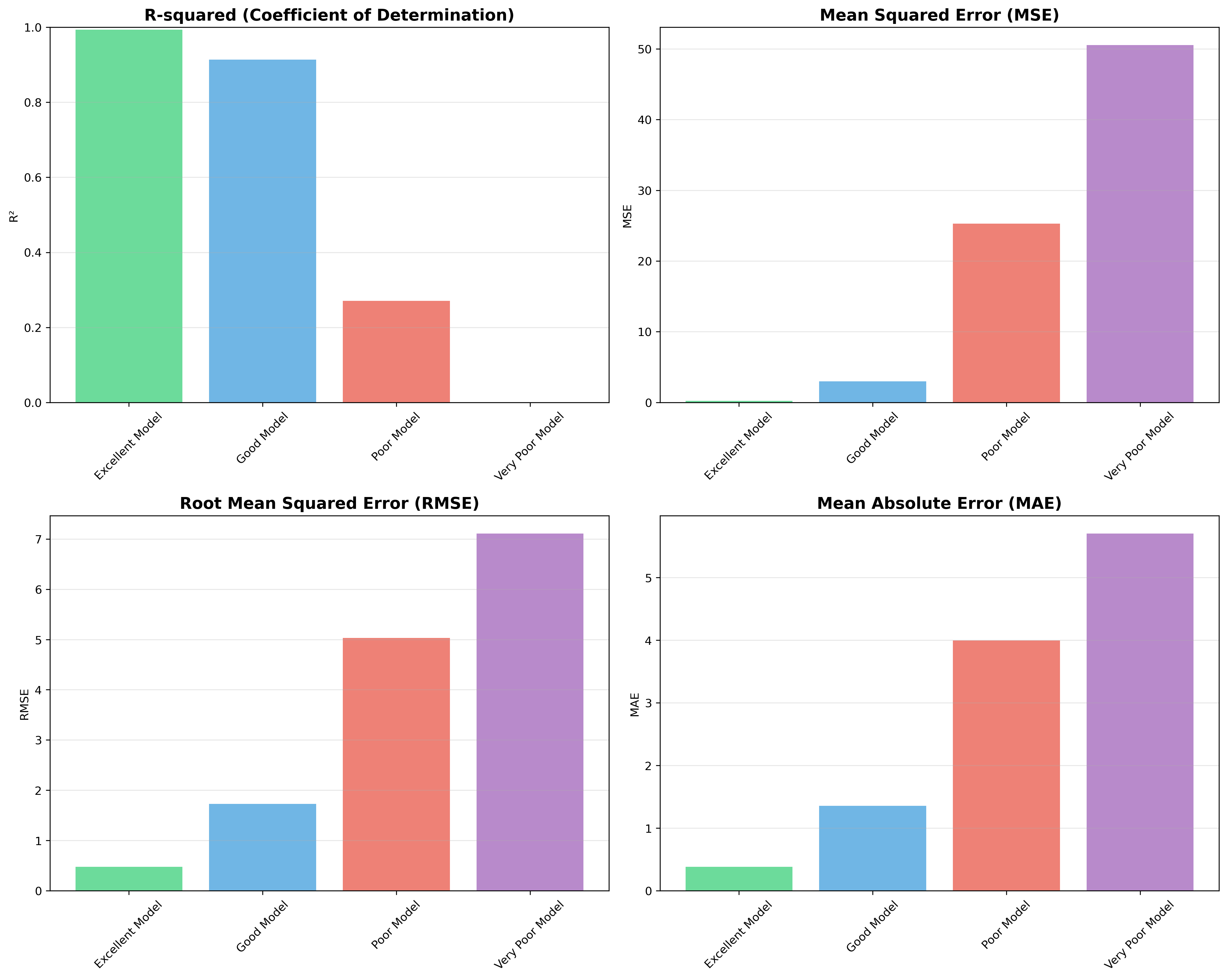
決定係数(R²)は最も一般的な評価指標の一つです。目的変数の変動のうち、回帰モデルで説明できる割合を表し、0から1の値を取ります。R²が高いほど、モデルの説明力が高いことを意味しますが、説明変数を追加すると必ずR²が向上するため、調整済み決定係数(Adjusted R²)も併せて確認することが重要です。
平均二乗誤差(MSE)は、予測値と実測値の差の二乗の平均を表します。MSEが小さいほど予測精度が高いことを示しますが、目的変数の単位の二乗になるため解釈が困難な場合があります。平均平方根誤差(RMSE)はMSEの平方根を取った値で、目的変数と同じ単位になるため解釈しやすくなります。
平均絶対誤差(MAE)は、予測値と実測値の差の絶対値の平均です。外れ値の影響を受けにくく、直感的に理解しやすい指標です。RMSEと比較して、MAEは外れ値に対してよりロバストな評価を提供します。これらの指標を効率的に計算するため、データ分析専用計算機や高性能グラフィック電卓の使用も検討できます。
平均絶対パーセント誤差(MAPE)は、誤差を目的変数に対する割合で表現する指標です。異なるスケールのデータを比較する際に有用ですが、目的変数が0に近い値を取る場合は不安定になる可能性があります。
情報量規準(AICやBIC)は、モデルの複雑さを考慮した評価指標です。これらの指標は、モデルの適合度と複雑さのトレードオフを評価し、過学習を避けながら最適なモデルを選択するのに役立ちます。AICは予測性能を重視し、BICは真のモデルの発見を重視する傾向があります。
クロスバリデーション(交差検証)は、モデルの汎化性能を評価する重要な手法です。データをトレーニングセットとテストセットに分割し、複数回の学習・評価を繰り返すことで、モデルの安定性を評価します。k-fold交差検証やLeave-One-Out交差検証などの手法があり、データサイズに応じて適切な手法を選択します。
ホールドアウト検証は、データを訓練用、検証用、テスト用に分割してモデルを評価する手法です。時系列データでは、時間的な順序を保持したタイムシリーズ分割を使用します。これらの高度な検証手法の実装には、機械学習実践ガイドが有用です。
過学習と汎化:バイアスと分散のトレードオフ
過学習(オーバーフィッティング)は機械学習と回帰分析において最も重要な概念の一つです。モデルが訓練データに過度に適合し、新しいデータに対する予測性能が低下する現象を指します。過学習の理解と対策は、実用的なモデル構築において不可欠です。
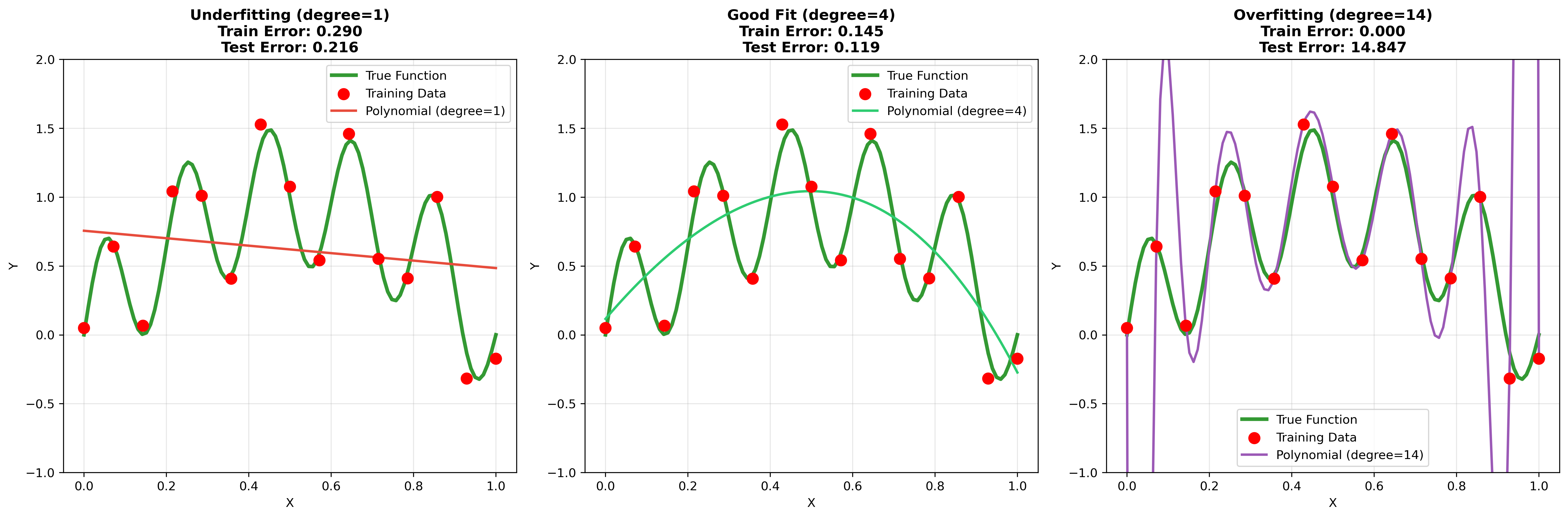
バイアス・バリアンス分解は、予測誤差を理論的に分析するフレームワークです。総誤差は、バイアス、分散、ノイズの三つの要素に分解できます。バイアスはモデルの系統的な誤差、分散はモデルの不安定性、ノイズは除去不可能な誤差を表します。優れたモデルは、これらの要素のバランスを最適化します。
未学習(アンダーフィッティング)は、モデルが単純すぎてデータのパターンを十分に捉えられない状態です。この場合、訓練データとテストデータの両方で性能が低くなります。モデルの複雑度を上げることで改善できますが、過学習とのバランスが重要です。
正則化は過学習を防ぐ最も一般的な手法です。L1正則化(Lasso)、L2正則化(Ridge)、エラスティックネット正則化などがあり、それぞれ異なる特性を持ちます。正則化パラメータの調整には、交差検証を用いたグリッドサーチやベイズ最適化などの手法を使用します。これらの高度な最適化手法の実装には、パラメータ最適化専門書が参考になります。
特徴選択は、重要な変数のみを選択することで過学習を防ぐ手法です。フィルタ法、ラッパー法、組み込み法などの手法があり、それぞれ異なるアプローチで最適な特徴量を選択します。遺伝的アルゴリズムや粒子群最適化などのメタヒューリスティック手法も特徴選択に応用されています。
次元削減は、主成分分析(PCA)や独立成分分析(ICA)などの手法を用いて、データの次元を削減しながら重要な情報を保持する技術です。高次元データにおける「次元の呪い」を回避し、計算効率と汎化性能の向上を両立できます。
早期停止(Early Stopping)は、反復的な学習アルゴリズムにおいて、検証誤差が増加し始めた時点で学習を停止する手法です。過学習を防ぎながら最適な学習を実現できます。深層学習や勾配ブースティングなどの手法でよく使用されます。
応用情報技術者試験での出題傾向と対策
応用情報技術者試験において、回帰分析は統計学、データベース、AI・機械学習の分野で頻繁に出題される重要トピックです。試験では、理論的な理解と実践的な応用能力の両方が評価されます。
午前問題では、回帰分析の基本概念、評価指標の意味、前提条件の理解などが問われます。決定係数R²の解釈、回帰係数の意味、残差分析の目的などに関する選択問題が出題されます。また、過学習の概念や正則化手法の効果についても理解が必要です。
午後問題では、具体的なビジネス場面での回帰分析の適用が問われます。売上予測、需要分析、リスク評価などの文脈で、適切な回帰手法の選択、結果の解釈、改善提案などを記述する問題が出題されます。これらの実践的な問題に対応するため、応用情報技術者試験対策書での学習が効果的です。
統計検定の理解も重要な要素です。t検定、F検定、カイ二乗検定などの基本的な統計検定の知識が、回帰分析の有意性検定において必要になります。これらの統計的概念の理解には、統計検定2級対策書が有用です。
データマイニングと機械学習の文脈での出題も増加傾向にあります。回帰分析を機械学習の教師あり学習として理解し、他の手法との比較や使い分けについて説明できることが求められます。データマイニング入門書での学習により、総合的な理解を深めることができます。
プログラミング的な観点からの出題も見られます。擬似コードや簡単なアルゴリズムの理解、計算量の評価などが問われる場合があります。PythonやRでの回帰分析の実装経験があると、これらの問題により効果的に対応できます。
実務での応用例を理解することも重要です。Webアクセス解析、在庫最適化、品質管理、金融リスク分析など、様々な分野での回帰分析の適用例を知ることで、応用問題に対する理解が深まります。これらの実践例は、ビジネス統計学実践書で学習できます。
実践的な実装とツール
現代の回帰分析は、高性能なソフトウェアとプログラミング言語を活用して行われます。適切なツールの選択と使い方の習得は、効率的で正確な分析を実現するために重要です。
PythonのScikit-learnは、機械学習における回帰分析の標準的なライブラリです。線形回帰、リッジ回帰、ラッソ回帰、多項式回帰など、様々な回帰手法を統一されたインターフェースで使用できます。データの前処理、モデルの訓練、評価までを一貫して行うことができ、初学者にも使いやすい設計になっています。
Rは統計解析に特化したプログラミング言語で、回帰分析に関する豊富なパッケージが提供されています。lm()関数による線形回帰、glm()関数による一般化線形モデル、多数の特殊な回帰手法などが利用可能です。統計的な結果の解釈や可視化においてRは特に優れており、学術研究でも広く使用されています。
SASやSPSSなどの商用統計ソフトウェアは、企業や研究機関で広く使用されています。GUIベースの操作により、プログラミング知識がなくても高度な分析を行うことができます。データの品質管理、大規模データの処理、レポート作成機能などが充実しており、実務での使用に適しています。これらのソフトウェアの習得には、統計ソフトウェア操作ガイドが有用です。
Excel等の表計算ソフトウェアでも基本的な回帰分析は可能です。データの可視化やシンプルな分析には適していますが、高度な統計処理や大量データの処理には限界があります。ビジネスでの簡易分析や教育目的では、Excel統計分析テンプレート集が実用的です。
クラウドベースの分析プラットフォームも普及しています。Google ColabやAzure Machine Learning Studioなどでは、高性能な計算リソースを使用した回帰分析が可能です。環境構築の手間が不要で、協業やシェアも容易です。
ビッグデータ処理にはApache SparkのMLlibやH2Oなどの分散処理フレームワークが使用されます。テラバイト級のデータに対しても効率的な回帰分析を実行でき、リアルタイム処理にも対応しています。これらの高度な技術の習得には、ビッグデータ分析技術書での学習が効果的です。
業界別の応用例と事例研究
回帰分析は様々な業界で実際に活用されており、それぞれの分野特有の課題や手法があります。業界別の応用例を理解することで、回帰分析の実践的な価値と可能性を把握できます。
マーケティング分野では、顧客の購買行動予測、価格弾力性分析、広告効果測定などに回帰分析が活用されています。RFM分析と組み合わせた顧客生涯価値(CLV)の予測、A/Bテストの結果分析、マーケットミックスモデリングなどが代表的な応用例です。デジタルマーケティングの発展により、リアルタイムでの分析と意思決定がより重要になっています。
金融業界では、信用リスク評価、株価予測、ポートフォリオ最適化、保険料算定などで回帰分析が中核的な役割を果たしています。ロジスティック回帰による信用スコアリング、時系列回帰による金利予測、VaRモデルによるリスク管理などが実用化されています。金融規制への対応や説明可能性の要求により、従来の統計手法の重要性が再認識されています。
製造業では、品質管理、需要予測、設備保全、工程最適化などで回帰分析が活用されています。統計的プロセス制御(SPC)、実験計画法と組み合わせた品質改善、予知保全システムの構築などが代表的な応用です。IoTセンサーからのリアルタイムデータを活用した回帰モデルにより、従来よりも精密な制御が可能になっています。
医療・ヘルスケア分野では、疾患リスク予測、治療効果分析、薬剤の用量反応関係の分析などに使用されています。臨床試験データの解析、電子健康記録(EHR)を活用した予後予測、ウェアラブルデバイスからの生体データ分析などが発展しています。医療分野特有の倫理的配慮や規制要件により、説明可能で検証可能なモデルの構築が重要です。
小売業界では、需要予測、価格最適化、在庫管理、店舗立地分析などで回帰分析が重要な役割を果たしています。POSデータとウェザーデータを組み合わせた需要予測、動的価格設定、サプライチェーン最適化などが実用化されています。オムニチャネル化により、オンラインとオフラインのデータを統合した分析が重要になっています。
エネルギー業界では、電力需要予測、再生可能エネルギーの出力予測、エネルギー価格分析などに回帰分析が活用されています。スマートグリッドの発展により、リアルタイムでの需給バランス調整や効率的な電力取引が可能になっています。これらの業界固有の応用例を深く学習するため、業界別データ分析事例集の活用が推奨されます。
新技術との融合と未来展望
回帰分析は伝統的な統計手法でありながら、現代の先端技術と融合することで新たな可能性を開拓しています。人工知能、機械学習、ビッグデータ技術との組み合わせにより、従来では不可能だった規模と精度での分析が実現されています。
深層学習との融合では、ニューラルネットワークの最終層に回帰出力を持つモデルが開発されています。畳み込みニューラルネットワーク(CNN)による画像からの数値予測、リカレントニューラルネットワーク(RNN)による時系列回帰などが実用化されています。これらの手法により、従来の線形回帰では捉えられない複雑なパターンも学習可能になっています。
自動機械学習(AutoML)技術により、回帰分析のプロセスが大幅に自動化されています。特徴量選択、モデル選択、ハイパーパラメータ調整、モデル評価までを自動化し、専門知識がなくても高品質な回帰モデルを構築できます。Google AutoML、H2O.ai、DataRobotなどの商用プラットフォームが提供されています。
説明可能AI(XAI)の発展により、複雑な機械学習モデルの予測結果を回帰分析的に解釈する技術が進歩しています。SHAP(SHapley Additive exPlanations)、LIME(Local Interpretable Model-agnostic Explanations)などの手法により、ブラックボックス化したモデルの動作を理解できます。
量子コンピューティングの応用研究も進んでいます。量子回帰アルゴリズムや量子最適化手法により、従来のコンピューターでは困難な大規模回帰問題の解決が期待されています。まだ研究段階ですが、将来的には画期的な性能向上が見込まれます。
エッジコンピューティング環境での回帰分析も重要な発展方向です。IoTデバイスや組み込みシステムでリアルタイムに回帰分析を実行する技術により、低遅延での意思決定が可能になります。フェデレーテッドラーニングと組み合わせることで、プライバシーを保護しながら分散学習も実現できます。
これらの最新技術動向を把握し、実務に活用するため、AI・機械学習最新技術書や量子コンピューティング入門書での継続学習が重要です。
まとめ:回帰分析の価値と重要性
回帰分析は、統計学と機械学習の基礎を成す重要な解析手法として、現代のデータドリブンな意思決定において不可欠な役割を果たしています。シンプルな単純回帰から高度な正則化回帰まで、様々な手法が用途に応じて使い分けられ、幅広い分野で実用的な価値を提供しています。
データサイエンスの基礎としての回帰分析の理解は、より高度な機械学習手法を学ぶ上での重要な土台となります。線形代数、確率論、統計学の基本概念が実践的に応用される回帰分析を通じて、データ分析の本質的な考え方を身につけることができます。
応用情報技術者試験においても、回帰分析は重要な出題分野であり、理論的な理解と実践的な応用能力の両方が求められます。試験対策を通じて得られる知識は、実務でのデータ分析業務に直接活用できる実用的な価値を持っています。
技術の進歩とともに、回帰分析の実装方法や応用範囲は継続的に拡大しています。伝統的な統計手法としての価値を保ちながら、最新の技術とも柔軟に融合し、新たな可能性を切り開いています。継続的な学習により、変化する技術環境に対応し、回帰分析の真価を最大限に活用することが可能になります。
データが企業や社会の貴重な資産となる現代において、回帰分析のスキルは専門職だけでなく、幅広いビジネスパーソンにとっても重要な能力となっています。適切な知識と実践経験により、データから価値ある洞察を抽出し、より良い意思決定を支援する能力を身につけることができます。