公開鍵暗号方式は、現代のデジタル社会において不可欠な暗号技術として、インターネット通信、電子商取引、デジタル署名などの基盤を支えています。従来の共通鍵暗号方式が抱えていた鍵配布問題を革新的に解決し、安全な通信を実現するこの技術は、応用情報技術者試験においても重要な出題分野となっています。本記事では、公開鍵暗号方式の基本概念から最新の技術動向まで、詳細かつ包括的に解説します。
公開鍵暗号方式の基本概念と歴史的発展
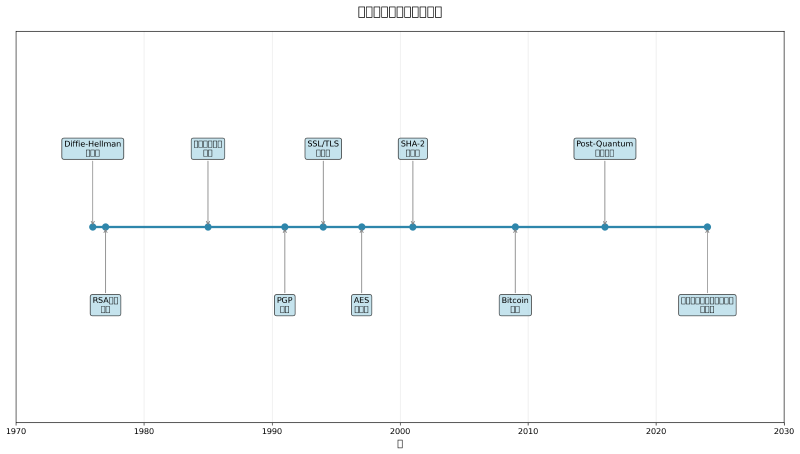
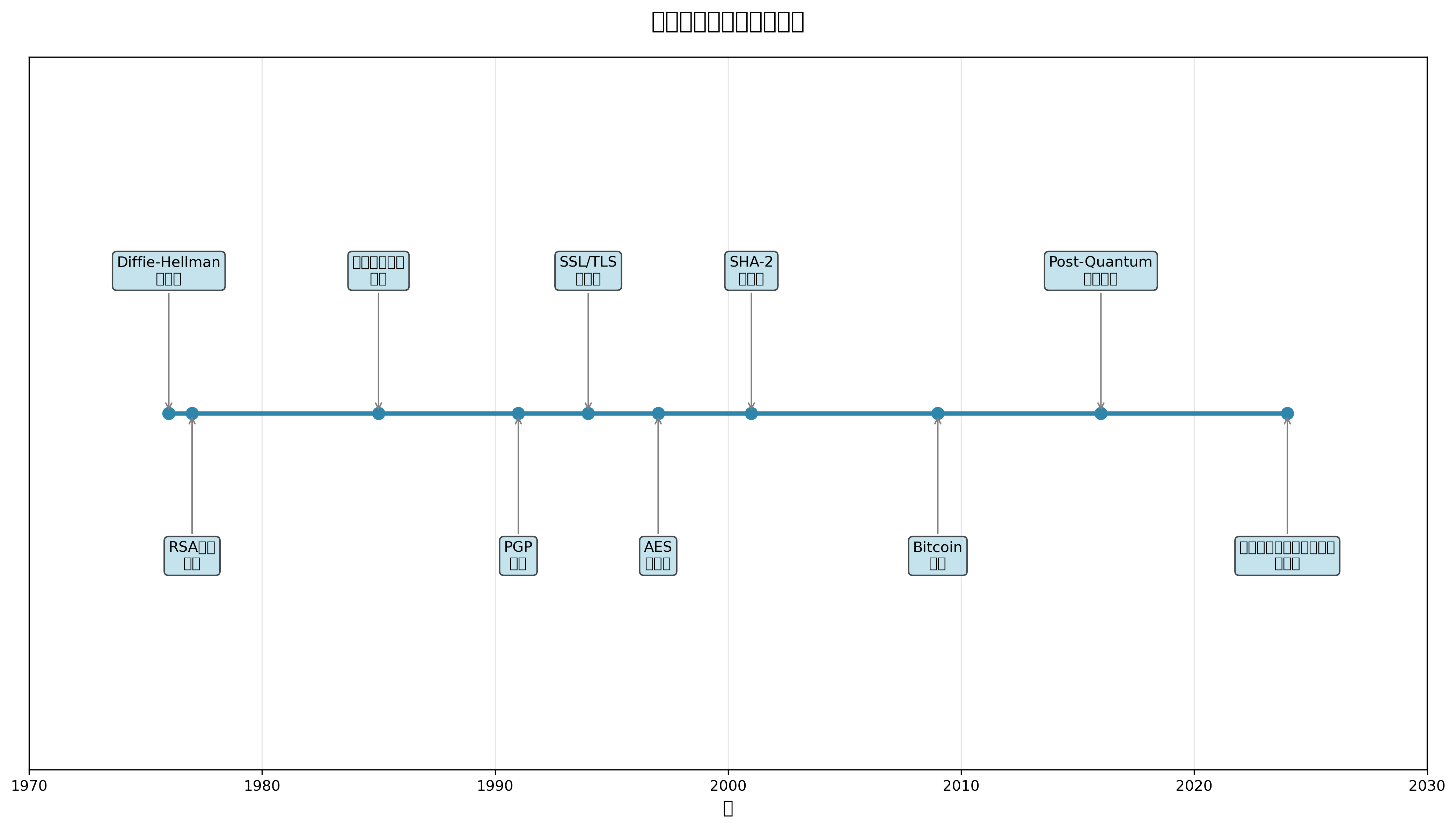
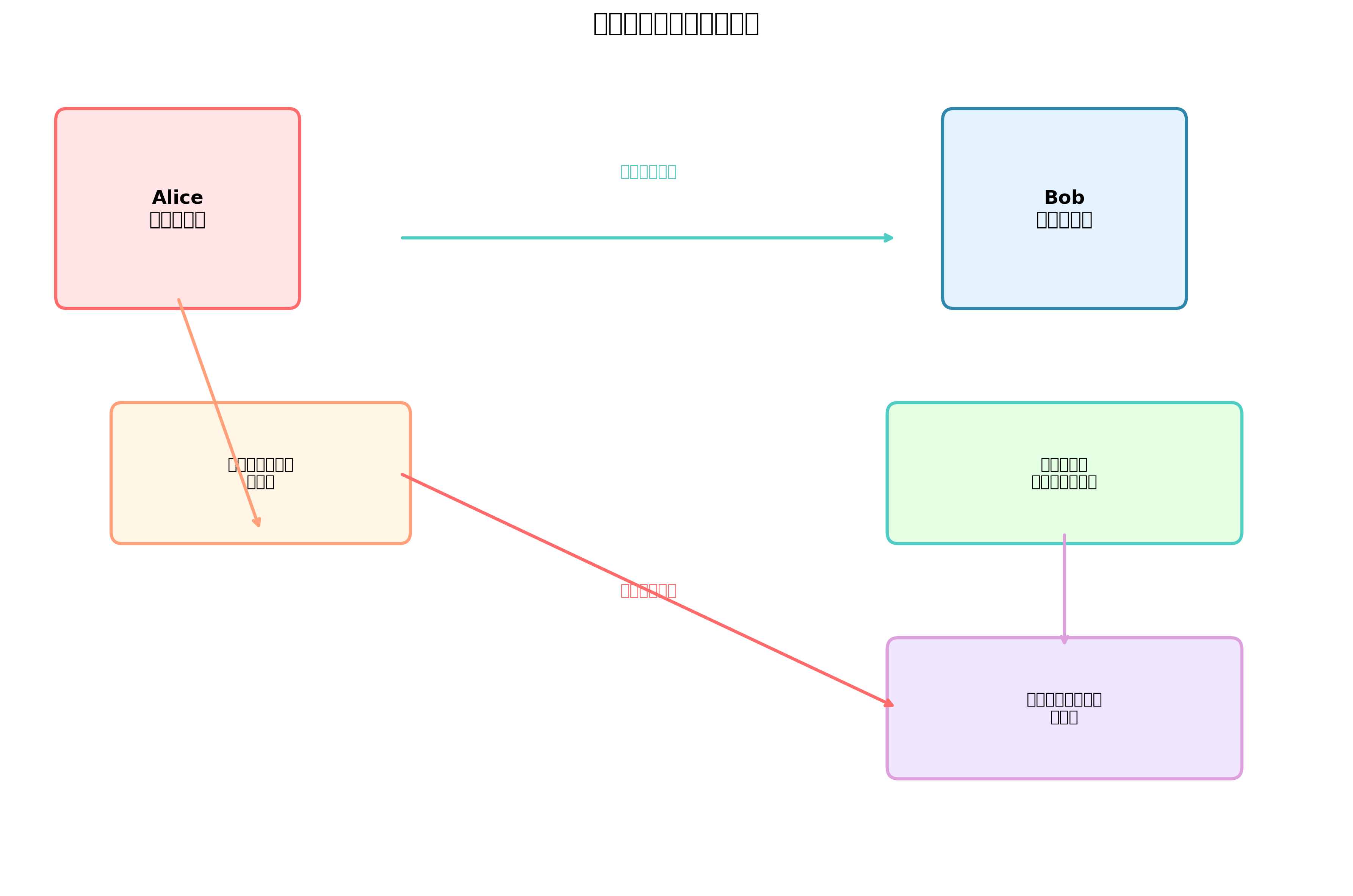
公開鍵暗号方式は、1976年にホイットフィールド・ディフィとマーティン・ヘルマンによって提案された革新的な暗号化技術です。この技術の最大の特徴は、暗号化に使用する鍵と復号化に使用する鍵が異なることにあります。暗号化に使用する公開鍵は広く公開され、復号化に使用する秘密鍵は所有者のみが保持します。このシステムにより、事前に鍵を共有することなく、安全な通信を開始できる画期的な仕組みが実現されました。
公開鍵暗号方式の登場以前は、通信を行う双方が同じ鍵を共有する必要がある共通鍵暗号方式が主流でした。しかし、この方式には致命的な鍵配布問題が存在していました。安全でない通信路を通じて鍵を共有することは、盗聴や改ざんのリスクを伴います。また、n人の参加者が相互に安全な通信を行うためには、n×(n-1)/2個の鍵が必要となり、参加者数の増加に伴って鍵管理が複雑化します。
暗号化技術の基礎書籍を参考に学習を進めることで、これらの基本概念をより深く理解できます。現代の情報社会では、インターネット上での情報交換が日常的に行われており、安全な通信を確保するための技術的基盤として公開鍵暗号方式の重要性は益々高まっています。
公開鍵暗号方式の数学的基盤は、一方向性関数という数学的特性に基づいています。一方向性関数は、順方向の計算は容易であるが、逆方向の計算は計算量的に困難な関数です。例えば、二つの大きな素数の積を求めることは比較的容易ですが、その積から元の素数を求めることは非常に困難です。この数学的特性を利用することで、公開鍵から秘密鍵を推測することが実質的に不可能となり、暗号系の安全性が保証されます。
公開鍵暗号方式の実用化には、計算効率の改善が重要な課題でした。初期の公開鍵暗号システムは、共通鍵暗号方式と比較して計算コストが高く、実用的な性能を得るためには様々な最適化が必要でした。現在では、ハードウェアの高性能化とアルゴリズムの改良により、実用的な性能を実現しています。高性能暗号処理装置を活用することで、大規模システムでも効率的な暗号化処理が可能となっています。
RSA暗号の詳細解説と実装
RSA暗号は、1977年にロナルド・リベスト、アディ・シャミア、レナード・エーデルマンによって発明された最も広く使用されている公開鍵暗号アルゴリズムです。RSA暗号の安全性は、大きな整数の素因数分解問題の困難性に基づいています。現在の計算機の能力では、十分に大きな合成数の素因数分解を実用的な時間内に行うことは不可能とされています。
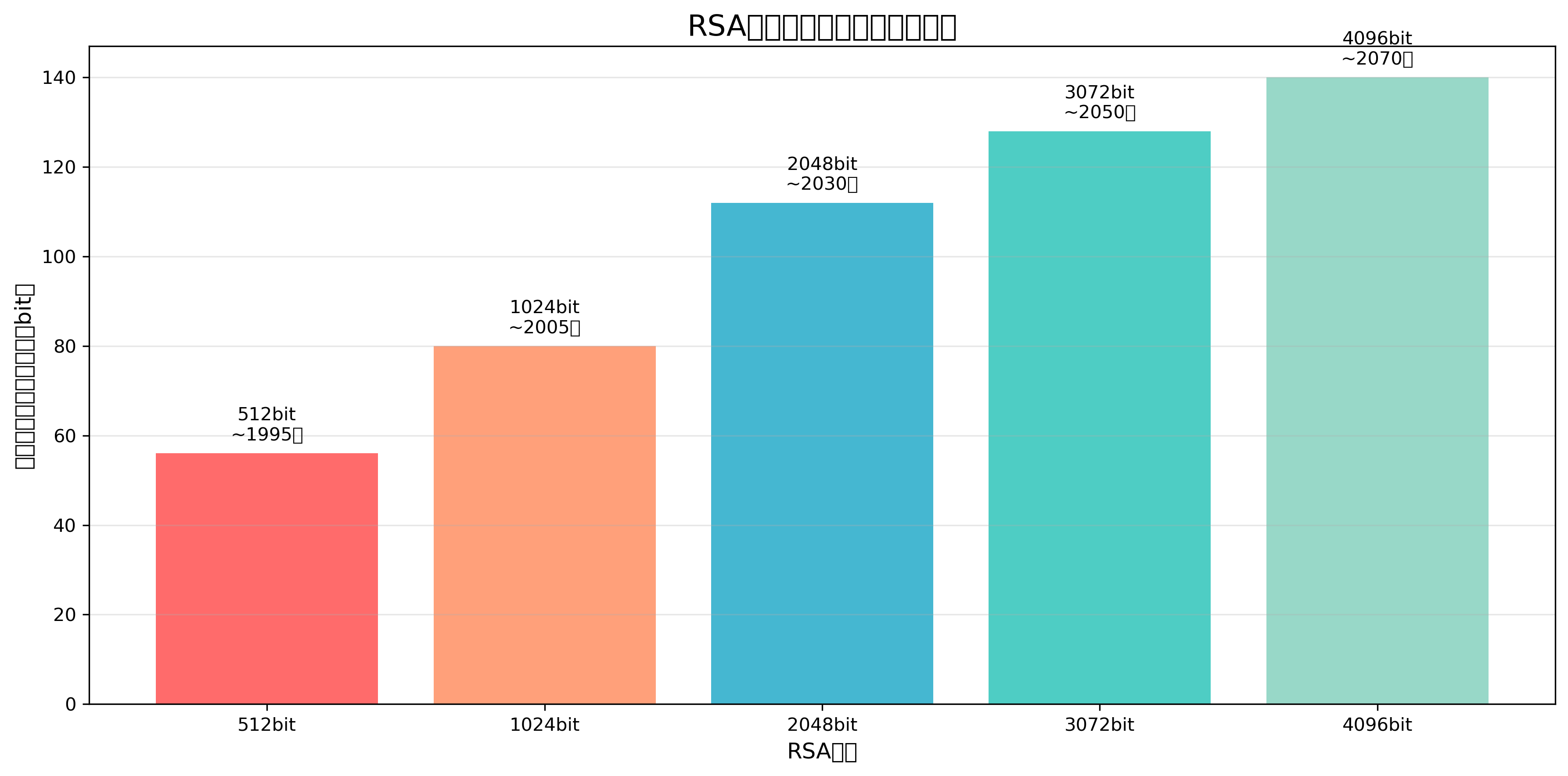
RSA暗号の鍵生成プロセスは、以下の手順で行われます。まず、二つの大きな素数pとqを選択します。これらの素数は、現在の標準では少なくとも1024ビット以上の長さを持つ必要があります。次に、これらの素数の積n = p × qを計算します。このnが公開鍵と秘密鍵の両方で使用される法数となります。続いて、オイラー関数φ(n) = (p-1)(q-1)を計算します。公開指数eは、φ(n)と互いに素な数として選択されます。一般的には、65537(216 + 1)が使用されます。最後に、ed ≡ 1 (mod φ(n))を満たす秘密指数dを計算します。
RSA暗号の暗号化プロセスでは、平文mを公開鍵(n, e)を使用してc = me mod nとして計算し、暗号文cを得ます。復号化プロセスでは、暗号文cを秘密鍵(n, d)を使用してm = cd mod nとして計算し、元の平文mを復元します。このプロセスの正確性は、オイラーの定理によって保証されています。
RSA暗号の実装において重要な考慮事項は、パディング方式の選択です。生のRSA暗号は、様々な攻撃に対して脆弱であるため、実際の実装では適切なパディング方式が使用されます。OAEP(Optimal Asymmetric Encryption Padding)やPKCS#1パディングなどの標準的なパディング方式により、暗号文の安全性が向上します。RSA暗号の実装ガイドを参考に、適切な実装方法を学習することが重要です。
現代のRSA暗号の鍵長は、セキュリティ要件に応じて選択されます。2048ビット鍵は現在の標準的な長さであり、2030年頃まで安全とされています。より長期間の安全性を求める場合は、3072ビット以上の鍵長が推奨されます。ただし、鍵長の増加に伴い計算コストも増加するため、性能要件とセキュリティ要件のバランスを考慮した選択が必要です。
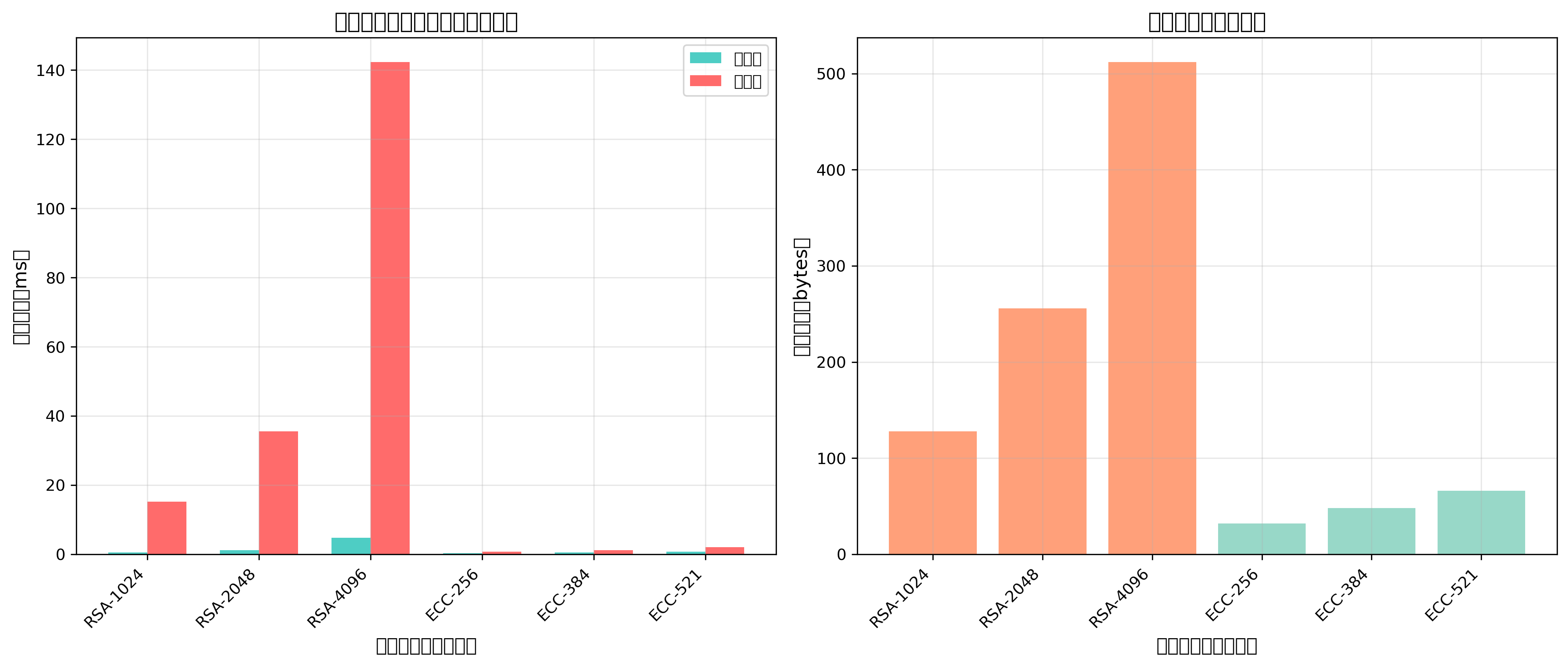
RSA暗号の計算効率を向上させるための技術として、中国剰余定理(CRT)を使用した高速化手法があります。CRTを使用することで、秘密鍵を使用した計算を約4倍高速化できます。この手法では、p-1とq-1を法とする計算を並列に実行し、結果を組み合わせることで最終的な結果を得ます。高速暗号計算技術の習得により、実用的な暗号システムの構築が可能となります。
RSA暗号は、デジタル署名にも広く使用されています。署名生成では、メッセージのハッシュ値を秘密鍵で暗号化し、署名検証では、署名を公開鍵で復号化して得られた値とメッセージのハッシュ値を比較します。この仕組みにより、メッセージの真正性と送信者の身元を確認できます。
楕円曲線暗号と次世代暗号技術
楕円曲線暗号(ECC)は、1985年にニール・コブリッツとビクター・ミラーによって独立に提案された公開鍵暗号方式です。楕円曲線暗号は、楕円曲線上の点の加法群における離散対数問題の困難性に基づいています。この方式の最大の利点は、RSA暗号と同等のセキュリティレベルを、より短い鍵長で実現できることです。
楕円曲線暗号で使用される楕円曲線は、y² = x³ + ax + b(mod p)の形で表現されます。ここで、aとbは楕円曲線のパラメータ、pは大きな素数です。楕円曲線上の点には、特殊な加法演算が定義されており、この演算により楕円曲線上の点の集合が群を形成します。楕円曲線暗号の安全性は、楕円曲線上の点Pに対して、kP = Qとなる整数kを求める問題(楕円曲線離散対数問題)の困難性に依存しています。
楕円曲線暗号の鍵生成プロセスでは、まず適切な楕円曲線とベースポイントGを選択します。秘密鍵は、1からn-1の範囲の乱数dとして選択されます。ここで、nはベースポイントGの位数です。公開鍵は、Q = dGとして計算されます。暗号化と復号化のプロセスは、選択されたスキームによって異なりますが、一般的にはECIES(Elliptic Curve Integrated Encryption Scheme)などの標準的な方式が使用されます。
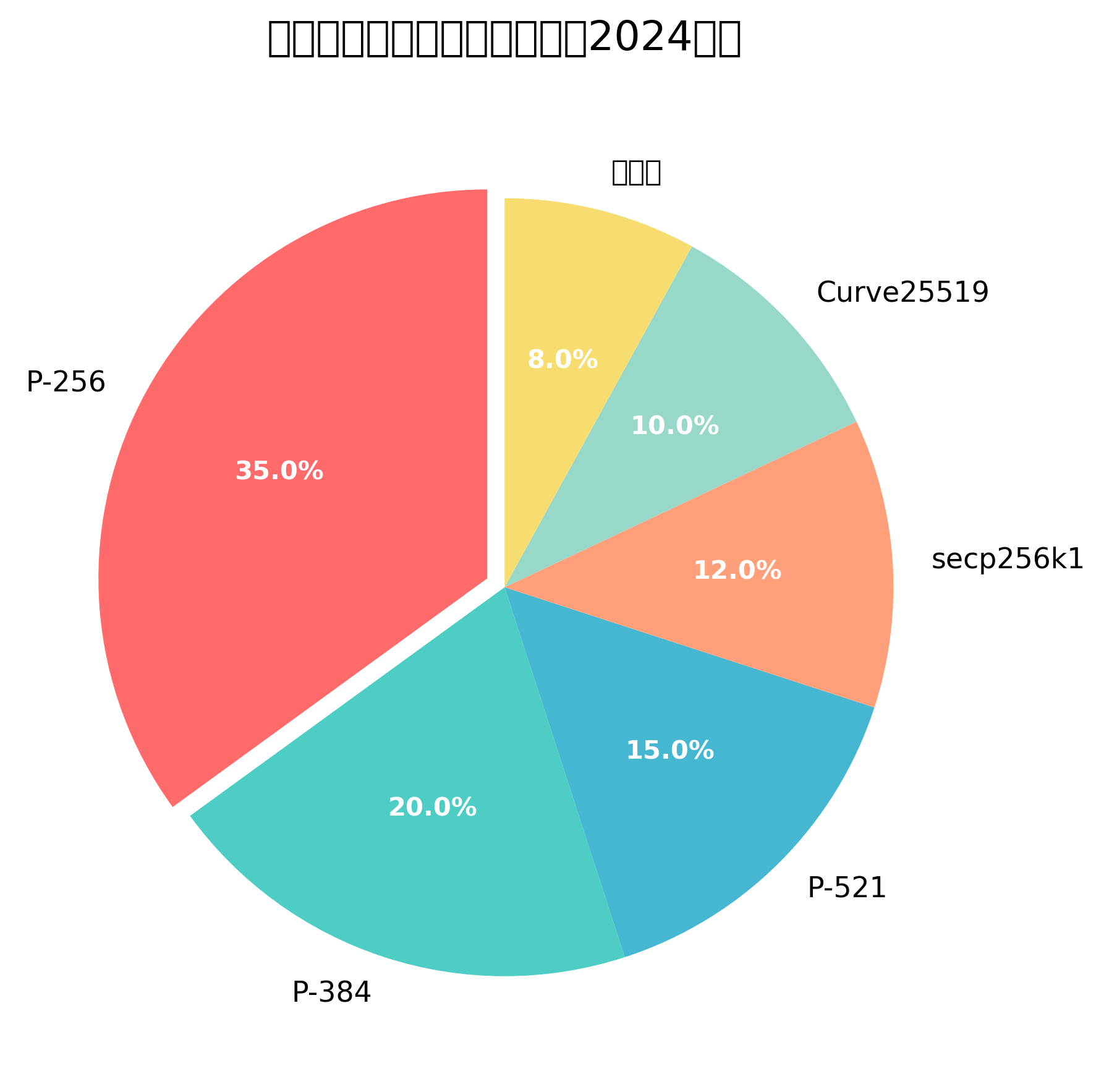
楕円曲線暗号の実装では、選択する楕円曲線のパラメータが重要な要素となります。NIST(米国国立標準技術研究所)が標準化したP-256、P-384、P-521曲線や、RFC7748で定義されたCurve25519、Curve448などが広く使用されています。これらの曲線は、セキュリティと性能のバランスを考慮して設計されており、実装の容易さと安全性を両立しています。楕円曲線暗号の実装技術に関する知識を深めることで、効率的で安全な暗号システムの構築が可能となります。
楕円曲線暗号の利点は、鍵のサイズが小さいことです。256ビットの楕円曲線鍵は、3072ビットのRSA鍵と同等のセキュリティレベルを提供します。これにより、メモリ使用量の削減、通信オーバーヘッドの低減、計算速度の向上が実現されます。特に、IoTデバイスや組み込みシステムなど、計算資源やメモリが限られた環境では、楕円曲線暗号の優位性が顕著に現れます。
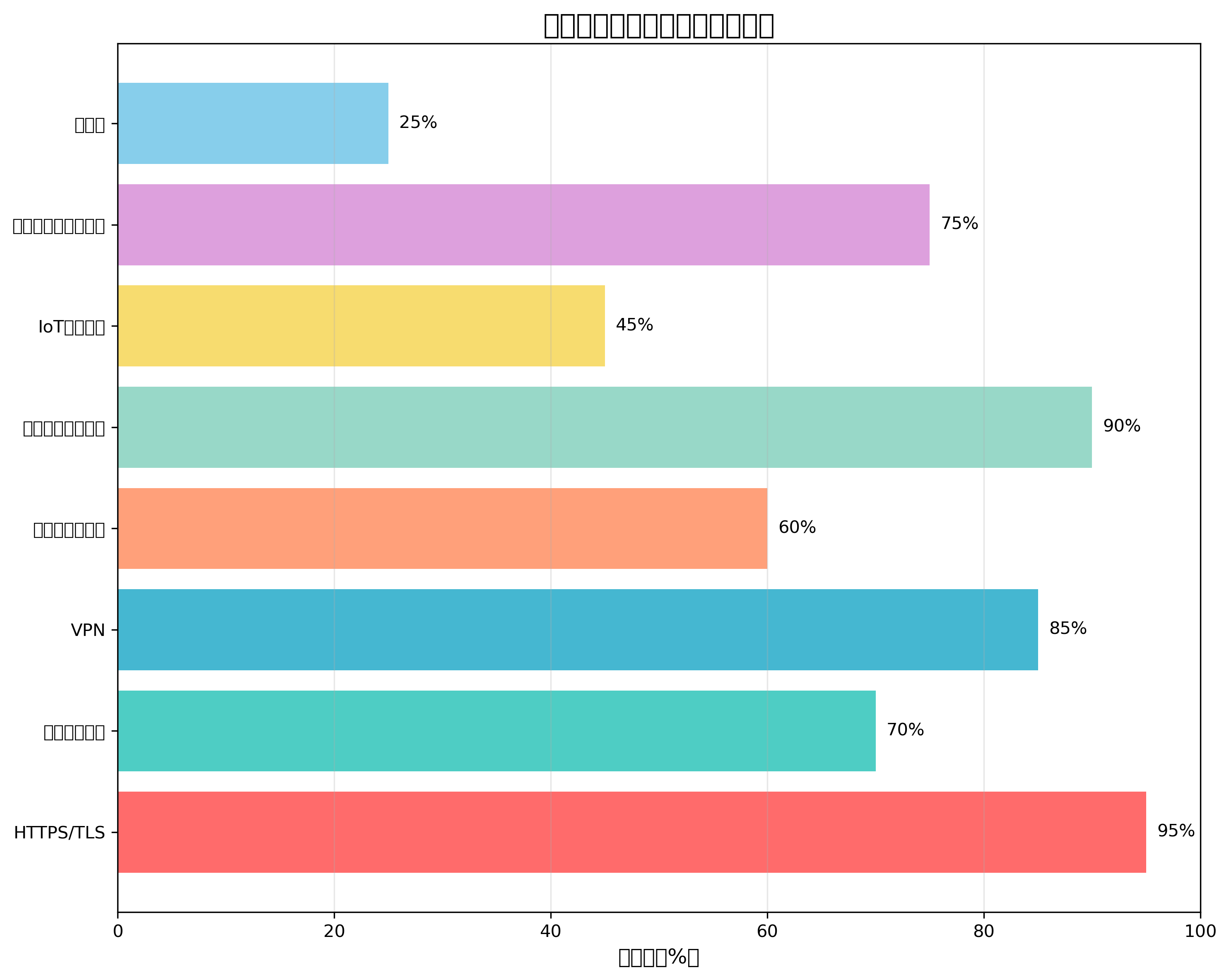
楕円曲線暗号は、現代の様々なプロトコルで採用されています。TLS/SSL通信では、ECDHE(Elliptic Curve Diffie-Hellman Ephemeral)鍵交換が使用され、前方秘匿性を提供します。ブロックチェーン技術では、ビットコインやイーサリアムなどの暗号通貨でsecp256k1曲線が使用されています。また、デジタル署名アルゴリズムとしてECDSA(Elliptic Curve Digital Signature Algorithm)が広く採用されています。
次世代の暗号技術として、耐量子暗号(Post-Quantum Cryptography)の研究開発が活発に行われています。量子コンピューターの発達により、RSA暗号や楕円曲線暗号の安全性が脅かされる可能性があるため、量子コンピューターに対しても安全な暗号方式の開発が急務となっています。NIST主導の標準化プロセスにより、格子ベース暗号、符号ベース暗号、多変数暗号などの候補が検討されています。
デジタル署名と認証技術の実装
デジタル署名は、公開鍵暗号方式を応用した重要な技術で、メッセージの真正性と送信者の身元を確認する機能を提供します。デジタル署名は、手書きの署名に相当するデジタル世界の機能として、法的な効力を持つ電子契約や公的文書の認証に使用されています。この技術により、否認防止、改ざん検出、送信者認証の三つの重要なセキュリティサービスが実現されます。
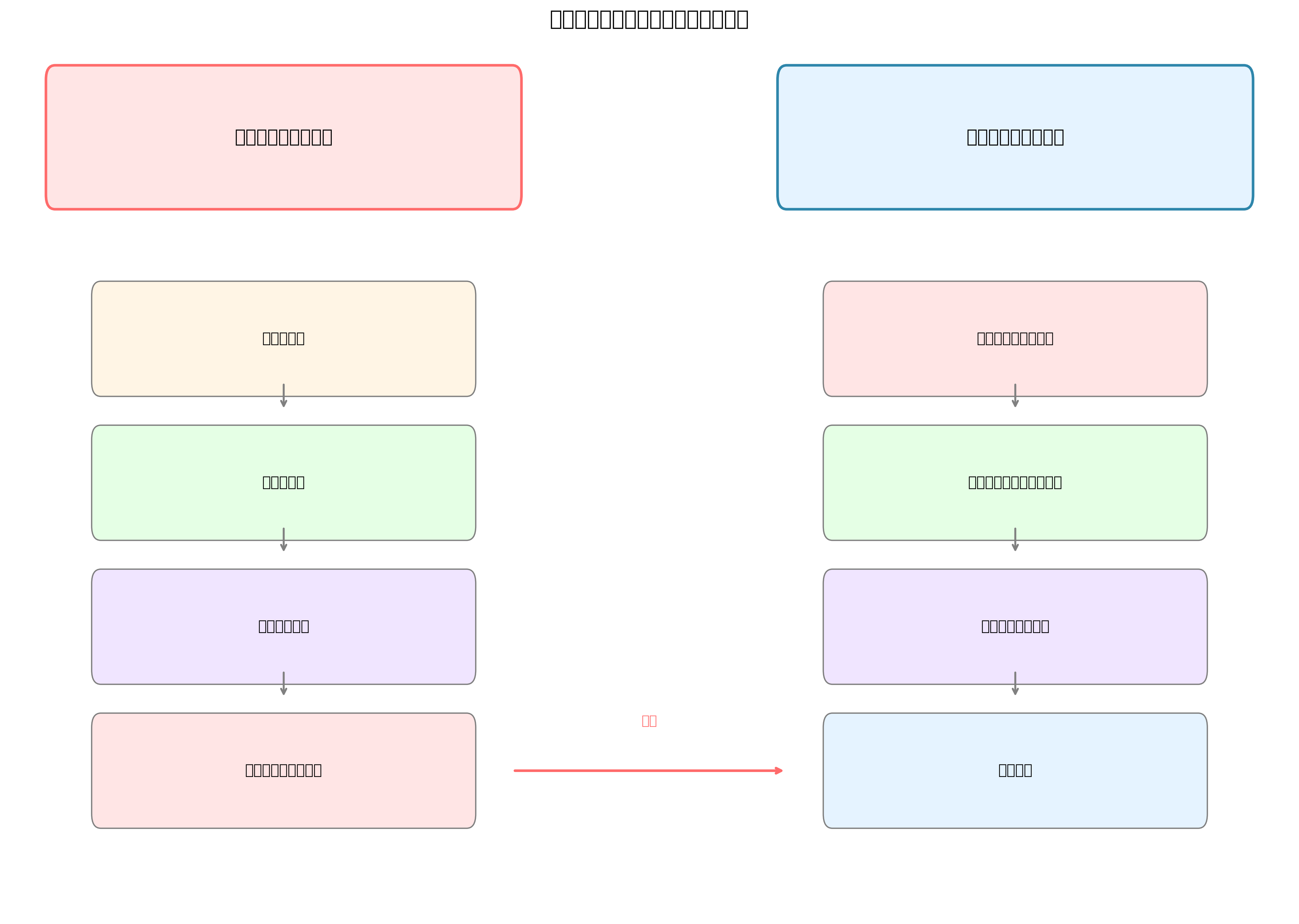
デジタル署名の生成プロセスは、以下の手順で行われます。まず、署名対象のメッセージに対してハッシュ関数を適用し、固定長のハッシュ値を生成します。使用されるハッシュ関数は、SHA-256、SHA-384、SHA-512などの暗号学的に安全な関数です。次に、生成されたハッシュ値を署名者の秘密鍵で暗号化し、デジタル署名を生成します。最後に、元のメッセージとデジタル署名を組み合わせて、署名付きメッセージを作成します。
デジタル署名の検証プロセスでは、受信者が署名付きメッセージを受け取った後、署名を送信者の公開鍵で復号化してハッシュ値を取得します。同時に、受信したメッセージに対して同じハッシュ関数を適用し、新たなハッシュ値を計算します。これら二つのハッシュ値が一致する場合、署名は有効であり、メッセージの真正性が確認されます。一致しない場合は、メッセージの改ざんまたは署名の偽造が疑われます。
RSAベースのデジタル署名では、PKCS#1やPSS(Probabilistic Signature Scheme)などの標準的なパディング方式が使用されます。これらのパディング方式により、署名の安全性が向上し、様々な攻撃に対する耐性が強化されます。デジタル署名の実装ガイドを参考に、適切な実装方法を学習することが重要です。
楕円曲線ベースのデジタル署名アルゴリズムであるECDSAは、高い効率性と安全性を提供します。ECDSAの署名生成では、楕円曲線上の点の演算を使用し、署名サイズを小さく抑えながら高いセキュリティレベルを維持します。EdDSA(Edwards-curve Digital Signature Algorithm)は、ECDSAの改良版として開発され、より高い性能と実装の容易さを提供します。
デジタル署名の実用化において重要な要素は、公開鍵の真正性を保証する公開鍵基盤(PKI)です。PKIは、デジタル証明書を使用して公開鍵と身元の関連付けを行い、信頼できる認証局(CA)がその関連付けを保証します。X.509デジタル証明書は、PKIの標準的な形式として広く使用されており、ウェブブラウザ、電子メール、VPNなどの様々なアプリケーションで活用されています。
タイムスタンプサービスは、デジタル署名の生成時刻を証明する重要な技術です。RFC3161で定義されたタイムスタンプトークンにより、署名の生成時刻を第三者が証明できます。これにより、証明書の有効期限切れ後でも、署名の有効性を確認できます。タイムスタンプシステムの導入により、長期間にわたる文書の信頼性を確保できます。
ブロックチェーン技術におけるデジタル署名は、取引の認証とスマートコントラクトの実行に不可欠な要素です。ビットコインでは、楕円曲線暗号を使用したデジタル署名により、取引の正当性を証明し、二重支払いを防止します。イーサリアムでは、スマートコントラクトの実行権限をデジタル署名により制御し、分散型アプリケーションの安全性を確保します。
量子コンピューティングと暗号技術の未来
量子コンピューティングの発展は、現在広く使用されている公開鍵暗号方式に対して根本的な脅威をもたらします。ピーター・ショアが1994年に発表したショアのアルゴリズムは、量子コンピューターを使用して大整数の素因数分解と離散対数問題を多項式時間で解く方法を示しました。この発見により、RSA暗号や楕円曲線暗号の安全性が将来的に脅かされる可能性が明らかになりました。
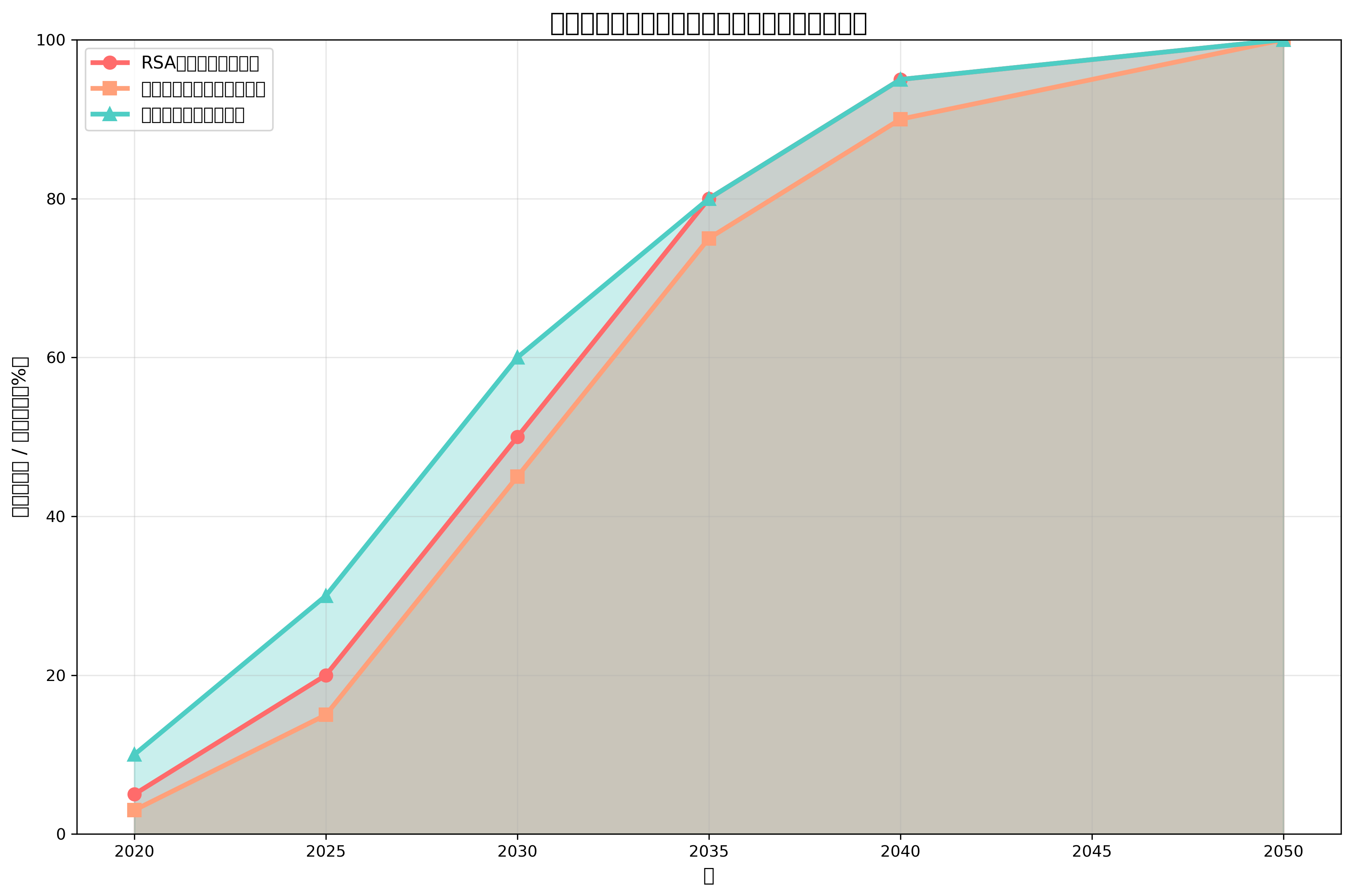
量子コンピューターの現在の技術レベルでは、実用的な暗号解読に必要な量子ビット数と量子ゲート数は未だ達成されていません。RSA-2048の解読には、約4096量子ビットの量子コンピューターが必要とされています。現在最先端の量子コンピューターは数百量子ビットの規模であり、実用的な暗号解読にはまだ時間がかかると予想されます。しかし、量子コンピューティング技術の急速な発展により、この脅威は現実のものとなりつつあります。
耐量子暗号の研究開発は、この量子脅威に対抗するための重要な取り組みです。NISTPQCプロジェクトでは、量子コンピューターに対しても安全な暗号アルゴリズムの標準化が進められています。2022年に発表された第1次標準化では、格子ベース暗号のKyber(鍵カプセル化)とDilithium(デジタル署名)が選定されました。これらのアルゴリズムは、数学的に異なる困難問題に基づいており、量子コンピューターでも解読が困難とされています。
量子コンピューティングと暗号技術の相互作用を理解することは、将来のセキュリティ戦略を立てる上で重要です。企業や組織は、量子コンピューターの実用化に備えて、現在のシステムから耐量子暗号への移行計画を策定する必要があります。この移行は、ハードウェアとソフトウェアの両方の観点から検討する必要があり、長期的な計画が必要です。
ハイブリッド暗号システムは、移行期間中の実用的な解決策として注目されています。このシステムでは、従来の暗号方式と耐量子暗号を組み合わせて使用し、どちらか一方が破られても安全性を維持できます。このアプローチにより、量子コンピューターの脅威に対する即座の対応と、将来的な完全移行への準備を両立できます。
量子鍵配送(QKD)は、量子力学の原理を利用した鍵配送技術です。この技術では、光子の量子状態を利用して鍵を配送し、盗聴の試みを物理的に検出できます。QKDは理論的には無条件安全性を提供しますが、実装上の制約や距離の制限などの課題があります。量子暗号技術の実装については、継続的な研究開発により実用化が進んでいます。
暗号プロトコルとセキュリティ標準
公開鍵暗号方式は、様々な暗号プロトコルの基盤技術として活用されています。TLS/SSL プロトコルは、インターネット通信のセキュリティを確保する最も重要なプロトコルの一つです。TLS 1.3では、楕円曲線暗号を使用したECDHE鍵交換により、前方秘匿性を実現しています。この機能により、長期間保存された通信記録が将来的に解読されても、過去の通信内容の安全性が保たれます。
IPSec(Internet Protocol Security)は、IP層でのセキュリティを提供するプロトコルスイートです。IPSecでは、IKE(Internet Key Exchange)プロトコルが鍵交換と認証を行い、ESP(Encapsulating Security Payload)がデータの暗号化と認証を行います。公開鍵暗号方式は、IKEプロトコルにおける相互認証とセッション鍵の安全な交換に使用されています。
S/MIME(Secure/Multipurpose Internet Mail Extensions)は、電子メールのセキュリティを確保するための標準です。S/MIMEでは、公開鍵暗号方式を使用してメールの暗号化とデジタル署名を行います。これにより、メールの機密性、完全性、真正性が保証されます。メール暗号化ソフトウェアを使用することで、企業や個人でも容易にセキュアなメール通信を実現できます。
PGP(Pretty Good Privacy)は、フィル・ジマーマンによって開発されたメールとファイルの暗号化システムです。PGPでは、RSA暗号や楕円曲線暗号を使用して、メッセージの暗号化とデジタル署名を行います。OpenPGPは、PGPの標準化版として広く使用されており、多くのメールクライアントやファイル暗号化ソフトウェアで採用されています。
SSH(Secure Shell)は、ネットワーク上でセキュアなリモートログインとファイル転送を行うためのプロトコルです。SSHでは、RSA、DSA、ECDSAなどの公開鍵暗号方式を使用してサーバー認証とクライアント認証を行います。また、鍵交換プロトコルにより、セッション暗号化のための共通鍵を安全に生成します。
実装上の考慮事項とベストプラクティス
公開鍵暗号方式を実装する際には、数多くの技術的考慮事項があります。まず、適切な鍵長の選択が重要です。現在の標準では、RSA暗号では2048ビット以上、楕円曲線暗号では256ビット以上の鍵長が推奨されています。将来的な安全性を考慮する場合は、より長い鍵長を選択することが望ましいです。
乱数生成の品質は、暗号システムの安全性に直接影響します。暗号学的に安全な乱数生成器(CSPRNG)を使用し、十分なエントロピーを確保することが不可欠です。特に、鍵生成時の乱数の品質は、システム全体の安全性を左右します。暗号学的乱数生成装置の導入により、高品質な乱数の生成が可能となります。
サイドチャネル攻撃に対する対策も重要な考慮事項です。電力解析攻撃、タイミング攻撃、電磁波解析攻撃などのサイドチャネル攻撃は、暗号化処理中に漏洩する物理的な情報を利用して秘密鍵を推測する攻撃手法です。これらの攻撃に対する対策として、定時間アルゴリズムの実装、電力消費の均一化、ノイズの注入などの技術が使用されます。
鍵管理は、暗号システムの運用において最も重要な要素の一つです。鍵の生成、配布、保存、更新、廃棄の各段階で適切なセキュリティ対策を実施する必要があります。HSM(Hardware Security Module)の使用により、鍵の安全な保存と処理が可能となります。HSMソリューションの導入により、企業レベルの鍵管理が実現できます。
証明書管理は、PKIシステムの運用において重要な要素です。証明書の発行、更新、失効の管理を適切に行うことで、システムの信頼性を維持できます。証明書失効リスト(CRL)やオンライン証明書状態プロトコル(OCSP)を使用することで、失効された証明書を適切に検出できます。
パフォーマンスの最適化は、実用的なシステムの構築において重要です。公開鍵暗号の計算コストは共通鍵暗号と比較して高いため、適切な最適化が必要です。ハードウェアアクセラレーション、並列処理、効率的なアルゴリズムの選択により、実用的な性能を実現できます。
新興技術と将来の発展
ブロックチェーン技術の発展により、公開鍵暗号方式の新たな応用分野が開拓されています。分散型アイデンティティ(DID)では、中央集権的な認証機関に依存せずに、個人がデジタルアイデンティティを管理できます。この技術により、プライバシー保護とセルフソブリン・アイデンティティが実現されます。ブロックチェーンセキュリティの理解は、現代の暗号技術者にとって重要な知識となっています。
同型暗号(Homomorphic Encryption)は、暗号化されたデータに対して直接計算を行うことができる革新的な技術です。この技術により、クラウドコンピューティング環境でデータの機密性を保護しながら計算処理を実行できます。完全同型暗号の実現により、プライバシー保護計算の新たな可能性が開かれています。
マルチパーティ計算(MPC)は、複数の参加者が秘密情報を共有することなく、合同で計算を実行する技術です。この技術により、医療データの共同分析、金融取引の処理、機械学習モデルの訓練などを、プライバシーを保護しながら実行できます。公開鍵暗号方式は、MPCプロトコルの重要な構成要素として使用されています。
ゼロ知識証明は、秘密を明かすことなく、その秘密を知っていることを証明する技術です。zk-SNARKsやzk-STARKsなどの効率的なゼロ知識証明システムの開発により、ブロックチェーン、認証システム、プライバシー保護技術への応用が拡大しています。ゼロ知識証明技術の学習により、最先端のプライバシー保護技術を理解できます。
セキュリティ脅威と対策
公開鍵暗号方式に対する攻撃手法は、技術の発展とともに高度化しています。数学的攻撃では、素因数分解アルゴリズムや離散対数問題の解法の改良により、暗号の解読が試みられます。一般数体篩法(GNFS)や楕円曲線法(ECM)などの古典的なアルゴリズムに加えて、量子アルゴリズムの発展により、新たな脅威が生まれています。
実装攻撃は、暗号アルゴリズムの数学的な強度ではなく、実装の脆弱性を悪用する攻撃手法です。タイミング攻撃では、暗号化処理の実行時間の変動を観測して秘密鍵を推測します。電力解析攻撃では、暗号処理中の電力消費パターンを解析して秘密情報を抽出します。これらの攻撃に対する対策として、マスキング技術や定時間実装などが使用されます。
社会工学的攻撃は、技術的な脆弱性ではなく、人間の心理的な弱点を悪用する攻撃手法です。フィッシング攻撃では、偽の電子メールやウェブサイトを使用して秘密鍵や認証情報を窃取します。証明書の偽造や認証局への侵入により、偽の証明書を発行する攻撃も報告されています。フィッシング対策セキュリティの実装により、これらの攻撃に対する防御が可能となります。
標準化と規制の動向
国際的な標準化機関では、公開鍵暗号方式の標準化が継続的に進められています。NIST(米国国立標準技術研究所)は、暗号アルゴリズムの標準化において主導的な役割を果たしており、FIPS(連邦情報処理標準)として暗号方式を規定しています。FIPS 186-5では、デジタル署名標準(DSS)として、RSA、DSA、ECDSAの仕様が定められています。
ISO/IECでは、国際標準として暗号技術の仕様を策定しています。ISO/IEC 9796シリーズでは、デジタル署名の国際標準を、ISO/IEC 18033シリーズでは、公開鍵暗号の国際標準を定めています。これらの標準により、国際的な相互運用性が確保されています。
IETF(Internet Engineering Task Force)では、インターネット上での暗号技術の使用に関する標準を策定しています。RFC(Request for Comments)として公開される文書により、TLS、IPSec、SSH、S/MIMEなどのプロトコルの仕様が定められています。これらの標準により、インターネット上での安全な通信が実現されています。
規制当局による暗号技術の規制も重要な要素です。各国の輸出管理規制により、暗号技術の輸出入が制限される場合があります。また、法執行機関による暗号解読の要求や、暗号技術の使用制限など、法的な制約も存在します。暗号技術の法的規制に関する知識は、国際的な事業展開において重要です。
教育と人材育成
公開鍵暗号方式の理解には、数学的な基礎知識が不可欠です。整数論、代数学、確率論などの数学的概念を理解することで、暗号アルゴリズムの動作原理を深く理解できます。また、計算複雑性理論の知識により、暗号の安全性評価が可能となります。暗号数学の基礎を学習することで、暗号技術の本質的な理解が深まります。
プログラミング技術も重要な要素です。暗号ライブラリの使用方法、セキュアなコーディング手法、暗号プロトコルの実装技術を習得することで、実用的な暗号システムの開発が可能となります。OpenSSL、Crypto++、Botan などの暗号ライブラリを使用した実装経験は、暗号技術者にとって重要なスキルです。
セキュリティ評価の手法も重要な知識です。暗号アルゴリズムの安全性評価、実装の脆弱性評価、システム全体のセキュリティ評価を行う能力が求められます。ペネトレーションテスト、コード監査、形式的検証などの手法を習得することで、より安全な暗号システムの構築が可能となります。
実用的な応用事例
企業における公開鍵暗号方式の実用的な応用事例として、電子契約システムがあります。電子契約では、デジタル署名により契約書の真正性を保証し、タイムスタンプにより契約締結時刻を証明します。このシステムにより、紙の契約書と同等の法的効力を持つ電子契約が実現されています。電子契約システムの導入により、業務効率化とコスト削減が実現されます。
クラウドストレージサービスでは、公開鍵暗号方式を使用してデータの暗号化と認証を行います。クライアント側で暗号化されたデータをクラウドに保存し、アクセス時にのみ復号化を行うことで、クラウドプロバイダーからもデータの内容を秘匿できます。エンドツーエンド暗号化により、高度なプライバシー保護が実現されています。
IoTデバイスのセキュリティでは、楕円曲線暗号が広く使用されています。計算資源とメモリが限られたIoTデバイスにおいて、楕円曲線暗号の効率性は重要な利点となります。デバイス認証、データ暗号化、ファームウェア更新の認証など、様々な用途で使用されています。IoTセキュリティソリューションの実装により、IoTシステムの安全性が確保されます。
公開鍵暗号方式は、現代デジタル社会の基盤技術として、今後も継続的な発展が期待されています。量子コンピューティングの脅威に対する耐量子暗号の研究開発、新たな応用分野の開拓、実装技術の向上など、多くの技術的課題に取り組む必要があります。応用情報技術者として、これらの最新動向を理解し、適切な技術選択と実装を行うことで、安全で信頼性の高い情報システムの構築に貢献できます。暗号技術の基礎から最新の研究動向まで、継続的な学習と技術習得により、変化する脅威環境に対応できる専門性を身につけることが重要です。