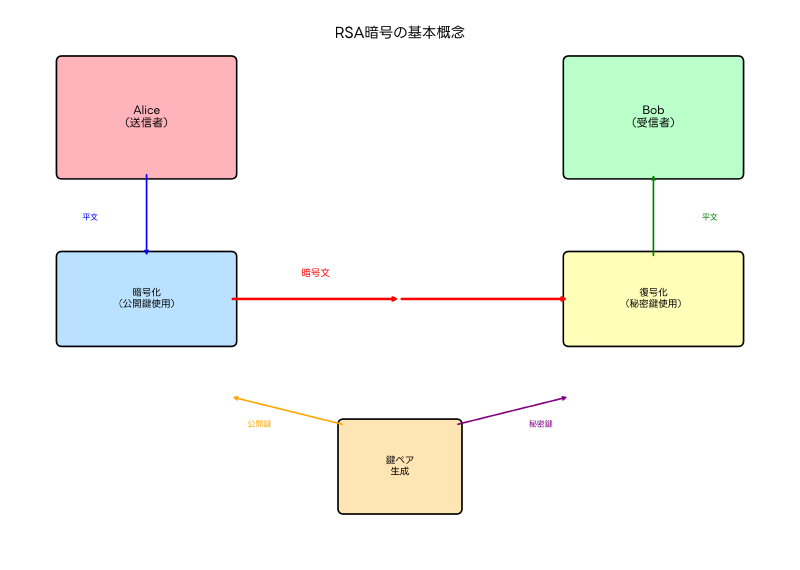
RSA暗号は、1977年にロン・リベスト(Ron Rivest)、アディ・シャミア(Adi Shamir)、レオナルド・エーデルマン(Leonard Adleman)によって開発された公開鍵暗号方式の代表格です。この暗号方式は、現代のインターネット社会において不可欠な基盤技術として、電子商取引、オンラインバンキング、電子メール、VPN接続など、あらゆる場面で使用されています。応用情報技術者試験においても最重要トピックの一つであり、暗号学の基礎から実装まで幅広い知識が求められる分野です。
RSA暗号の最大の特徴は、暗号化に使用する鍵と復号化に使用する鍵が異なる「非対称暗号」である点です。この革新的なアプローチにより、事前に秘密の鍵を共有することなく、安全な通信を確立することが可能になりました。公開鍵は文字通り公開され、誰でもその鍵を使って暗号化を行うことができますが、復号化は対応する秘密鍵を持つ者のみが行うことができます。
RSAの数学的基盤と鍵生成プロセス
RSA暗号の安全性は、大きな合成数の素因数分解が計算量的に困難であるという数学的事実に基づいています。現在のコンピュータ技術では、十分に大きな数の素因数分解には天文学的な時間が必要であり、これがRSAの暗号学的強度の源泉となっています。
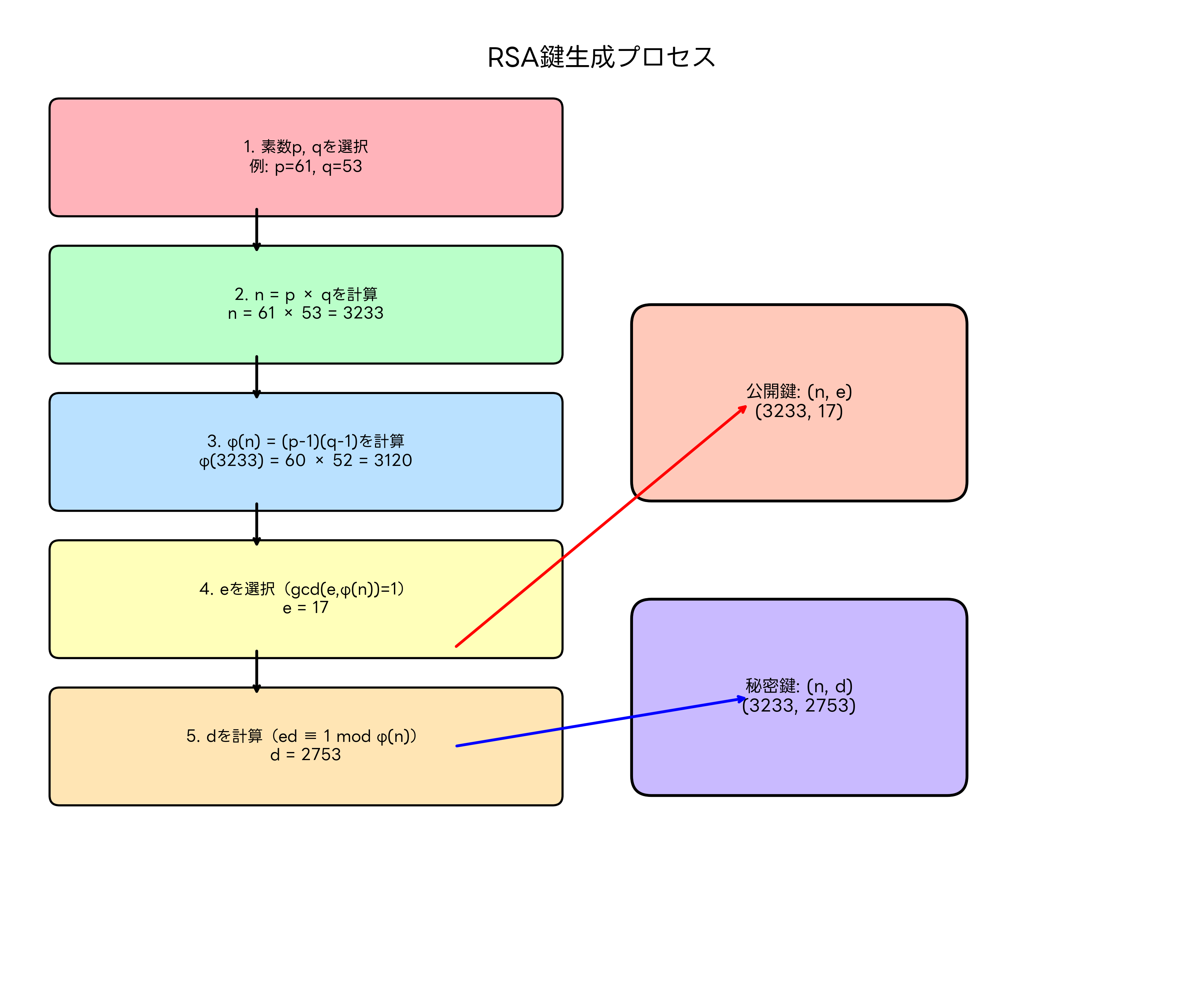
鍵生成プロセスは以下の手順で行われます。まず、二つの大きな素数pとqを選択します。これらの素数は通常、1024ビット以上の長さを持ち、現在では2048ビット以上が推奨されています。高性能な素数生成ソフトウェアを使用することで、暗号学的に安全な素数を効率的に生成できます。
次に、n = p × q を計算します。この値nは公開鍵と秘密鍵の両方に含まれ、RSA暗号の「法」として機能します。続いて、オイラーのφ関数φ(n) = (p-1)(q-1) を計算します。この値は鍵生成プロセスでのみ使用され、生成後は安全に削除されます。
公開指数eを選択する際は、1 < e < φ(n) かつ gcd(e, φ(n)) = 1 を満たす値を選びます。一般的にe = 65537 = 2^16 + 1が使用されます。この値は暗号化の高速化と安全性のバランスを考慮して選ばれています。最後に、拡張ユークリッド互除法を用いて ed ≡ 1 (mod φ(n)) を満たす秘密指数dを計算します。
現代の暗号システムでは、専用の暗号化ハードウェアを使用して、鍵生成プロセスを高速化し、安全性を向上させることが一般的です。これらのハードウェアは、真の乱数生成機能や改ざん防止機能を備えており、より堅牢な暗号システムの構築を可能にします。
暗号化と復号化の仕組み
RSAの暗号化と復号化は、モジュラー冪乗演算に基づいて行われます。平文メッセージMを暗号化する際は、受信者の公開鍵(n, e)を使用して、暗号文C = M^e mod n を計算します。この暗号文Cは、対応する秘密鍵を持つ受信者のみが復号できます。
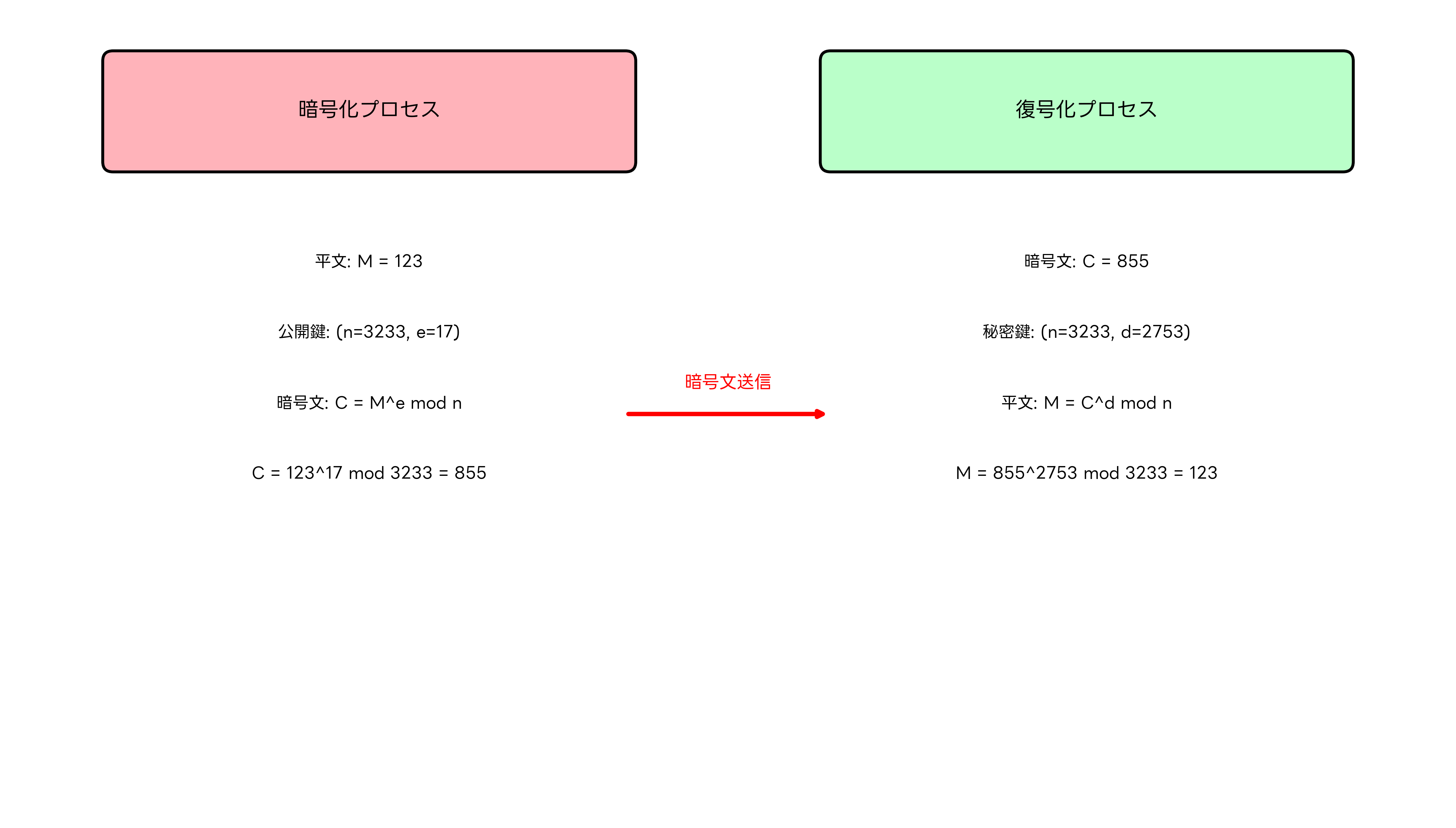
復号化プロセスでは、受信者が秘密鍵(n, d)を使用して、M = C^d mod n を計算することで元の平文を復元します。この数学的な関係は、オイラーの定理とフェルマーの小定理に基づいており、正しい秘密鍵を持つ者のみが確実に復号できることを保証します。
実際の暗号化では、平文のサイズがnよりも小さくなるよう調整が必要です。長いメッセージを暗号化する場合は、平文を適切なサイズのブロックに分割するか、より効率的なハイブリッド暗号システムを使用します。ハイブリッド暗号では、RSAで共通鍵を暗号化し、実際のデータは高速な共通鍵暗号で処理する方法が採用されています。
モジュラー冪乗演算の計算には、効率的なアルゴリズムが不可欠です。特に、バイナリ法(二進法)や中国人剰余定理を活用することで、計算時間を大幅に短縮できます。高性能数値計算ライブラリを使用することで、これらの複雑な演算を効率的に実行できます。
RSAのセキュリティ強度と鍵長の選択
RSAの安全性は、使用する鍵長に大きく依存します。鍵長が長いほど素因数分解が困難になり、より高いセキュリティレベルを提供しますが、同時に計算コストも増大します。現在の技術水準では、1024ビット以下のRSA鍵は安全性が不十分とされ、2048ビット以上の使用が強く推奨されています。
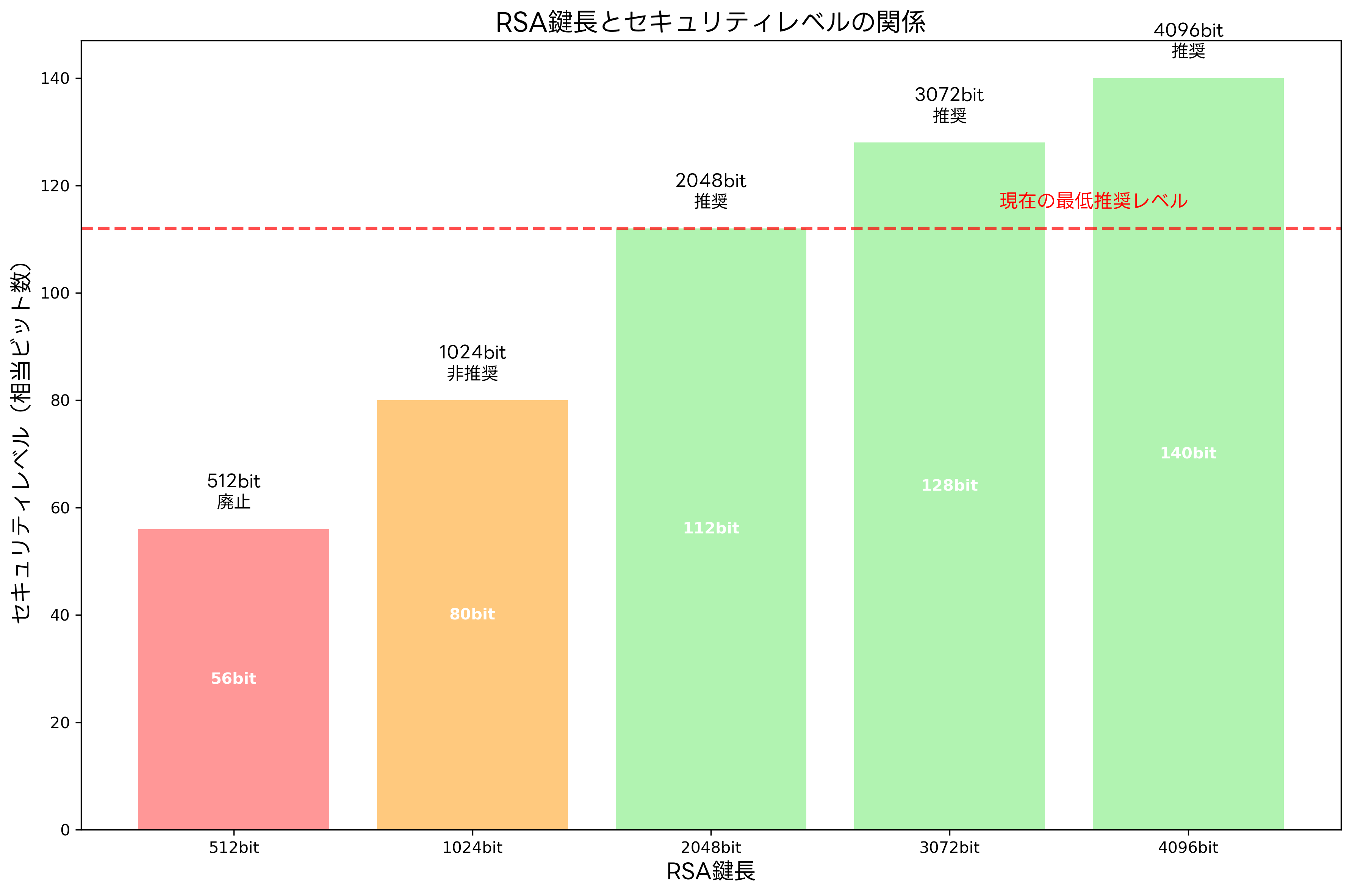
NIST(米国国立標準技術研究所)の推奨では、2048ビットRSAは112ビットの対称鍵暗号と同等のセキュリティレベルを提供します。金融機関や政府機関などの高度なセキュリティが要求される環境では、3072ビットまたは4096ビットのRSA鍵が使用されることが多くなっています。
量子コンピューティングの発展により、RSAの将来的な安全性に対する懸念が高まっています。十分に強力な量子コンピュータが実用化された場合、ショア(Shor)のアルゴリズムにより、現在のRSA暗号は破られる可能性があります。この脅威に対応するため、量子暗号対応セキュリティシステムの研究開発が活発化しており、ポスト量子暗号への移行準備が進められています。
鍵長の選択においては、セキュリティ要件、性能要件、システムの寿命を総合的に考慮する必要があります。暗号強度評価ツールを使用することで、特定の用途に最適な鍵長を科学的に決定できます。
他の暗号方式との比較と特徴
RSAは公開鍵暗号の代表的な方式ですが、他の暗号方式と比較すると独特の特徴を持っています。対称暗号のAESと比較すると、RSAは暗号化・復号化の処理速度が大幅に劣りますが、鍵配送問題を解決できるという大きな利点があります。
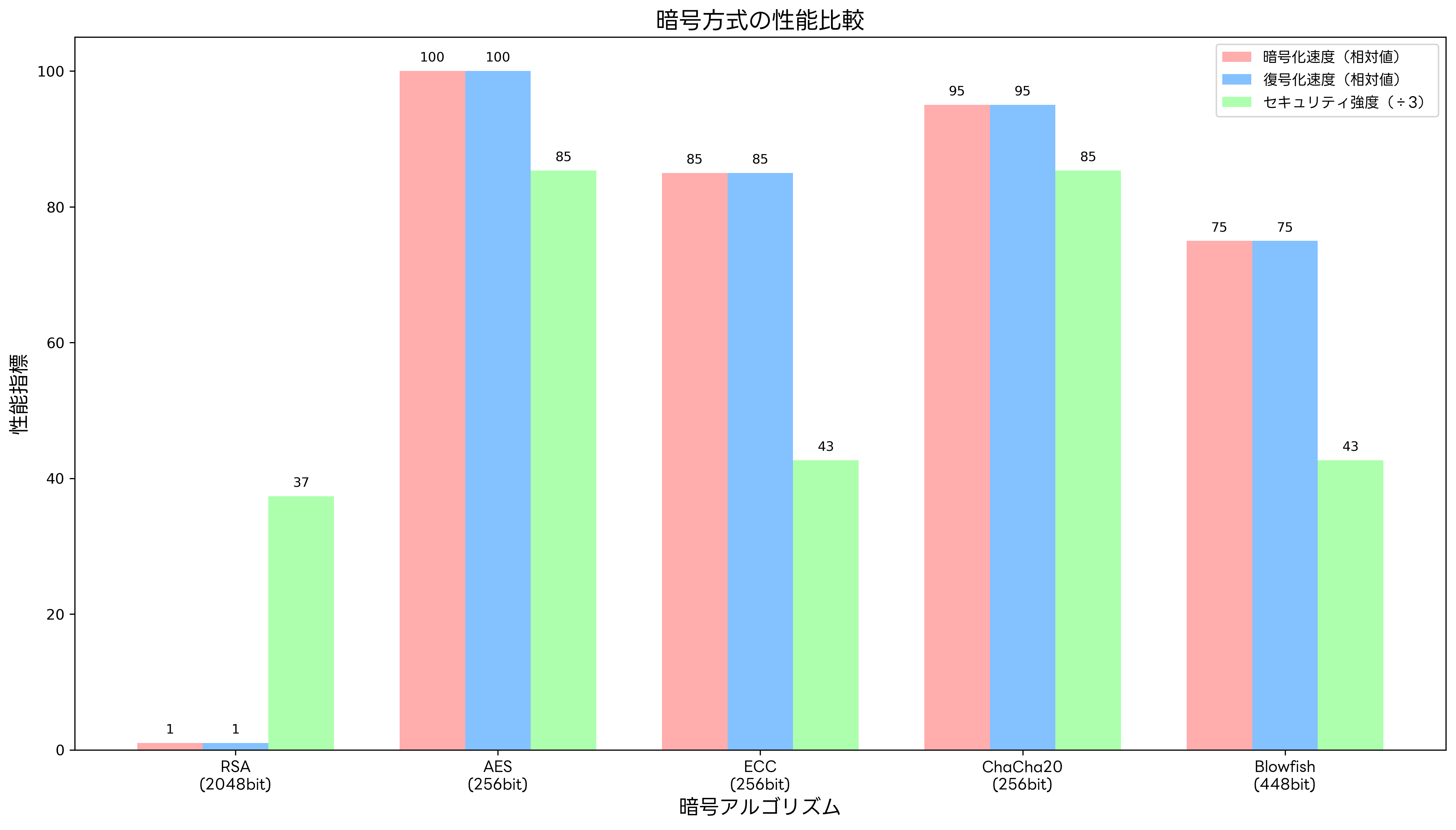
楕円曲線暗号(ECC)と比較すると、RSAは鍵長が長く、計算コストが高いという欠点がありますが、実装の歴史が長く、多くのシステムでの実績があることが利点です。また、RSAは数学的基盤が理解しやすく、実装が比較的容易であるため、教育現場や研究機関で広く使用されています。
暗号方式比較分析ソフトウェアを使用することで、特定の用途に最適な暗号方式を選択する際の意思決定を支援できます。システムの要件に応じて、速度、セキュリティ、実装の容易さなどの要因を総合的に評価することが重要です。
ChaCha20やBlowfishなどの現代的なストリーム暗号と比較すると、RSAは暗号化速度で大きく劣りますが、デジタル署名や認証といった公開鍵暗号特有の機能を提供できます。これらの機能は、現代の情報システムにおいて不可欠であり、RSAが広く採用される理由となっています。
RSAの実用的な応用分野
RSA暗号は、現代のデジタル社会において極めて広範囲な応用分野を持っています。最も重要な応用の一つがSSL/TLS通信であり、HTTPS接続において必要不可欠な技術として使用されています。Webブラウザとサーバー間の初期認証や鍵交換において、RSAの公開鍵暗号機能が活用されています。
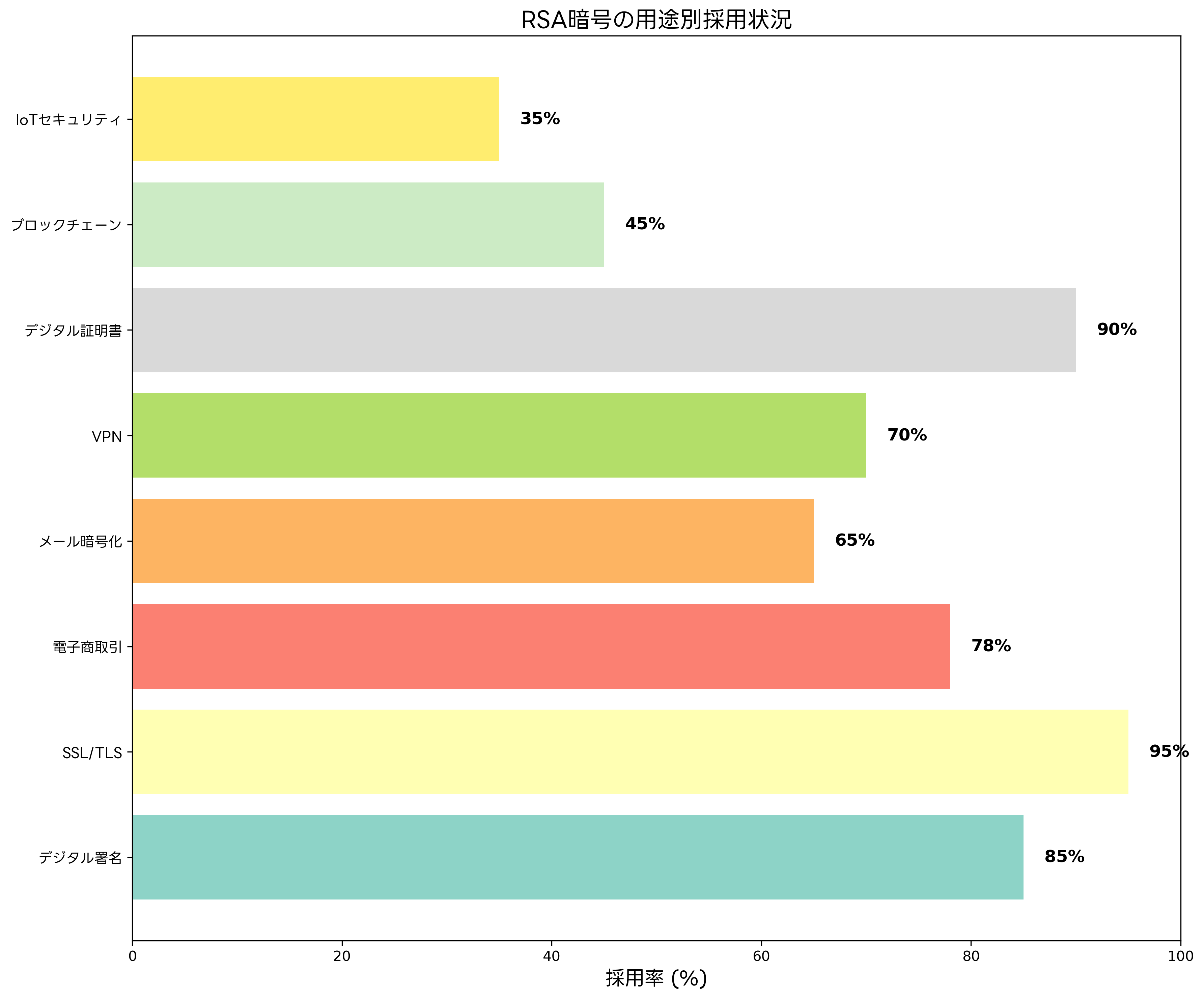
電子商取引の分野では、オンライン決済システムにおいてRSAが重要な役割を果たしています。クレジットカード情報の暗号化、デジタル署名による取引の真正性確保、認証局によるデジタル証明書の発行など、電子商取引の安全性を支える基盤技術となっています。
デジタル署名は、RSAの最も重要な応用の一つです。文書の改ざん検出、送信者の身元確認、否認防止などの機能を提供し、電子契約や公的文書の電子化において不可欠な技術となっています。デジタル署名ソリューションを導入することで、紙ベースの業務プロセスを電子化し、効率性と安全性を両立できます。
電子メールセキュリティの分野では、PGPやS/MIMEなどのシステムでRSAが活用されています。メールの暗号化、デジタル署名、送信者認証などの機能により、機密情報を含むメール通信の安全性を確保できます。企業向けメールセキュリティシステムの多くがRSAベースの暗号化機能を提供しています。
VPN(Virtual Private Network)システムにおいても、RSAは重要な役割を果たしています。VPNクライアントとサーバー間の初期認証、鍵交換、証明書ベースの認証などでRSAが使用されています。企業向けVPNソリューションを選択する際は、RSAのサポート状況と実装品質を重要な評価基準とすべきです。
デジタル証明書とPKI(公開鍵基盤)
RSA暗号の実用化において、デジタル証明書とPKI(Public Key Infrastructure)の役割は極めて重要です。デジタル証明書は、公開鍵の真正性を証明する電子的な証明書であり、信頼できる第三者機関(認証局)によって発行されます。この仕組みにより、通信相手の身元確認と公開鍵の正当性検証が可能になります。
認証局(CA:Certificate Authority)は、デジタル証明書の発行、管理、失効処理を行う重要な機関です。VeriSign、DigiCert、Let’s Encryptなどの主要認証局が、世界中のWebサイトやシステムに対してデジタル証明書を提供しています。企業向け証明書管理システムを導入することで、組織内でのデジタル証明書の一元管理と自動更新が可能になります。
証明書チェーン(Certificate Chain)は、ルート証明書から中間証明書、最終的なエンドエンティティ証明書に至る信頼の連鎖を構築します。この階層構造により、世界中の異なるシステム間での相互認証が実現されています。証明書の検証プロセスでは、有効期限、失効状況、発行者の信頼性などが総合的にチェックされます。
証明書失効リスト(CRL:Certificate Revocation List)とOCSP(Online Certificate Status Protocol)は、失効した証明書を識別するメカニズムです。秘密鍵の漏洩や組織の変更などにより証明書が無効になった場合、これらの仕組みにより迅速に失効情報が配布されます。証明書ライフサイクル管理ツールを使用することで、証明書の発行から失効まで全てのプロセスを効率的に管理できます。
RSAの脆弱性と攻撃手法
RSAの安全性は数学的な困難問題に基づいていますが、実装上の問題や側面チャネル攻撃などにより脆弱性が生じる可能性があります。最も基本的な攻撃手法は素因数分解攻撃ですが、適切な鍵長を使用することで現実的な時間内での攻撃を困難にできます。
パディング攻撃は、RSAの実装における重要な脆弱性の一つです。特に、PKCS#1 v1.5パディングを使用したRSA暗号化では、Bleichenbacher攻撃などの適応的暗号文攻撃が可能となります。この問題を解決するため、OAEP(Optimal Asymmetric Encryption Padding)などの安全なパディング方式の使用が推奨されています。
側面チャネル攻撃は、暗号化処理の実行時間、消費電力、電磁波などの物理的な情報を利用して秘密鍵を推定する攻撃手法です。セキュリティ評価・テストツールを使用して、実装の安全性を定期的に検証することが重要です。
タイミング攻撃は、RSA復号化の処理時間の違いから秘密鍵の情報を取得する攻撃です。この攻撃を防ぐため、処理時間を一定にするブラインド化技術や、Montgomery reduction などの攻撃耐性のあるアルゴリズムが使用されています。暗号処理高速化ハードウェアを使用することで、攻撃に対する耐性を向上させながら性能も改善できます。
実装時の重要な考慮事項
RSAを実際のシステムに実装する際は、多くの技術的考慮事項があります。乱数生成の品質は、RSAの安全性を左右する最も重要な要素の一つです。暗号学的に安全な疑似乱数生成器(CSPRNG)を使用し、十分なエントロピーを確保することが不可欠です。
鍵管理システムの設計では、鍵の生成、保存、分配、更新、廃棄の全ライフサイクルを考慮する必要があります。ハードウェアセキュリティモジュール(HSM)を使用することで、秘密鍵の安全な保存と暗号処理の実行が可能になります。
性能最適化の観点では、中国人剰余定理(CRT)を活用した高速復号化、モンゴメリー乗算による効率的なモジュラー演算、マルチプレシジョン演算ライブラリの選択などが重要です。数学計算最適化ライブラリを適切に選択することで、処理速度の大幅な向上が期待できます。
マルチスレッド環境での実装では、スレッドセーフティの確保、共有リソースの適切な管理、パフォーマンスの最適化が課題となります。現代の並列処理対応暗号ライブラリを使用することで、マルチコア環境でのRSA処理を効率化できます。
応用情報技術者試験での出題傾向と対策
応用情報技術者試験においては、RSA暗号に関する問題が情報セキュリティ分野で頻出しています。午前問題では、RSAの基本原理、鍵生成プロセス、暗号化・復号化の計算、セキュリティ強度、他の暗号方式との比較などが問われます。
計算問題では、小さな数値を使ったRSA暗号化・復号化の実例が出題されることが多く、モジュラー演算の理解が重要です。例えば、p=3, q=11の場合のn, φ(n), e, dの計算や、実際の暗号化・復号化の計算過程を求める問題が出題されています。数学的基礎力強化問題集を活用して、モジュラー演算の習熟度を高めることが効果的です。
午後問題では、より実践的な観点からRSAの応用が問われます。PKI、デジタル署名、SSL/TLS、電子商取引などの文脈で、RSAの役割と適切な実装方法に関する理解が評価されます。企業のセキュリティ戦略立案、暗号化システムの設計、セキュリティインシデントの分析などの場面でRSAの知識を応用する能力が求められます。
試験対策としては、応用情報技術者試験セキュリティ分野専門書で理論的基礎を固め、暗号学演習問題集で計算問題の解法を習得することが重要です。また、実際のシステムでの暗号実装経験があると、午後問題での理解が深まります。
量子コンピューティング時代への対応
量子コンピューティング技術の進歩により、RSA暗号の長期的な安全性に対する懸念が高まっています。ショアのアルゴリズムは、十分に強力な量子コンピュータが実現された場合、現在のRSA暗号を効率的に破ることができる理論的基盤を提供しています。
この脅威に対応するため、NIST(米国国立標準技術研究所)はポスト量子暗号の標準化プロセスを進めています。格子暗号、符号理論、多変数暗号、同種写像暗号などの新しい数学的困難問題に基づく暗号方式が研究され、一部は既に標準化されています。ポスト量子暗号研究書籍を通じて、これらの新技術への理解を深めることが重要です。
ハイブリッド暗号システムの概念も重要性を増しています。現在のRSAベースシステムとポスト量子暗号を組み合わせることで、移行期間中のセキュリティを確保しながら、将来的な量子攻撃にも対応できます。暗号移行管理システムを使用することで、段階的な暗号方式の移行を効率的に管理できます。
企業や組織は、量子コンピューティング時代に向けた準備として、現在の暗号資産の棚卸し、リスク評価、移行計画の策定を進める必要があります。量子リスク評価ツールを活用して、組織のシステムがどの程度の量子脅威にさらされているかを定量的に評価することが推奨されます。
まとめ
RSA暗号は、現代のデジタル社会を支える最も重要な暗号技術の一つです。その数学的な美しさと実用性の高さから、開発から45年以上が経過した現在でも、世界中のシステムで広く使用されています。応用情報技術者試験においても、RSAの理解は情報セキュリティ分野での成功に不可欠な要素となっています。
RSAの基本原理である素因数分解問題の困難性は、現在のコンピュータ技術では克服が困難ですが、量子コンピューティングの発展により、将来的な脅威が現実のものとなりつつあります。この変化に対応するため、ポスト量子暗号への移行準備と、ハイブリッドシステムの構築が重要な課題となっています。
技術者として、RSAの理論的理解だけでなく、実装時の考慮事項、セキュリティ上の注意点、性能最適化手法についても深く学ぶことが重要です。また、PKIやデジタル証明書との関係、他の暗号方式との相互運用性についても理解を深め、総合的な暗号システムの設計能力を身につけることが求められます。
現代の情報社会において、暗号技術は単なる技術的な要素を超えて、社会インフラとしての役割を担っています。RSA暗号の深い理解を通じて、安全で信頼性の高い情報システムの構築に貢献し、デジタル社会の発展に寄与することが、私たち技術者の重要な使命といえるでしょう。