現代社会において、統計学は様々な分野で重要な役割を果たしています。ビジネスの意思決定から医学研究、品質管理、マーケティング分析まで、データに基づいた客観的判断を支える基盤として不可欠な学問です。応用情報技術者試験においても、統計学に関する知識は頻出テーマであり、システム開発における品質評価やデータ分析の理論的基盤として重要視されています。
統計学は、データの収集、整理、分析、解釈を通じて、不確実性の中から有用な情報を抽出する科学的手法です。記述統計学と推測統計学の二つの大きな分野に分けられ、それぞれが異なる目的と手法を持っています。記述統計学はデータの特徴を要約し可視化することに重点を置き、推測統計学は標本から母集団について推論することを目的としています。
記述統計学:データの特徴を明らかにする
記述統計学は、収集したデータの特徴を数値や図表を用いて要約し、理解しやすい形で表現する分野です。この分野の基本となる概念には、中心傾向の尺度(平均値、中央値、最頻値)、散らばりの尺度(範囲、分散、標準偏差)、分布の形状を表す指標(歪度、尖度)があります。
平均値は最も一般的な中心傾向の指標ですが、外れ値の影響を受けやすいという特徴があります。そのため、データに極端な値が含まれる場合には、中央値の方が適切な代表値となることがあります。例えば、所得分布のように一部の高所得者が平均を押し上げる場合、中央値の方が一般的な所得水準をより正確に表現します。
散らばりの尺度では、標準偏差が最も重要な指標です。標準偏差は、データがどの程度平均値から離れているかを示し、データの信頼性や一貫性を評価する際に重要な役割を果たします。品質管理における統計的工程管理ツールでは、標準偏差を基準とした管理図が広く使用されており、製造プロセスの安定性を監視しています。
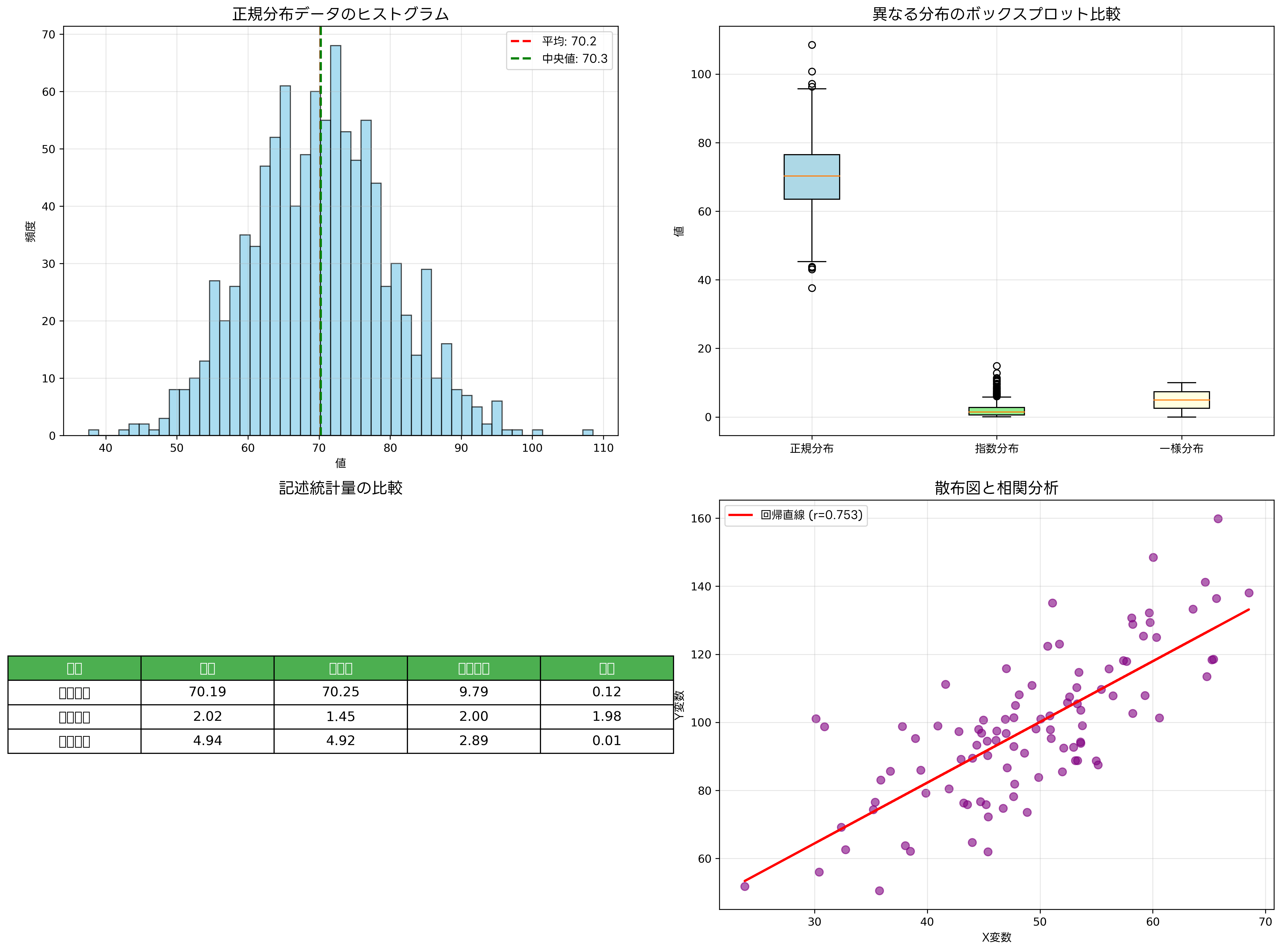
データの視覚化は記述統計学の重要な要素です。ヒストグラム、散布図、ボックスプロット、円グラフなどの図表を使用することで、数値だけでは理解しにくいデータの特徴やパターンを明確に把握できます。現代のデータ分析では、統計解析ソフトウェアやデータ可視化ツールを活用することで、効率的かつ高品質な分析が可能になっています。
相関分析は、二つの変数間の関係の強さと方向を調べる手法です。相関係数は-1から1の間の値を取り、1に近いほど強い正の相関、-1に近いほど強い負の相関を示します。ただし、相関関係があることと因果関係があることは異なる概念であり、相関の解釈には注意が必要です。マーケティング分析では、顧客行動分析ツールを使用して、商品売上と広告投資額の相関関係を分析し、効果的なマーケティング戦略を策定しています。
確率論の基礎:不確実性を数学的に扱う
確率論は統計学の理論的基盤を提供する重要な分野です。確率は0から1の間の値で表され、事象が起こる可能性の度合いを定量的に表現します。確率の基本法則には、加法定理、乗法定理、条件付き確率の定理があり、これらを理解することで複雑な確率問題を体系的に解決できます。
確率分布は、確率変数が取りうる値とその確率の関係を表現する概念です。離散確率分布と連続確率分布に分類され、それぞれ異なる特徴を持っています。二項分布、ポアソン分布、正規分布、指数分布など、各分布は特定の状況や現象をモデル化するのに適しています。
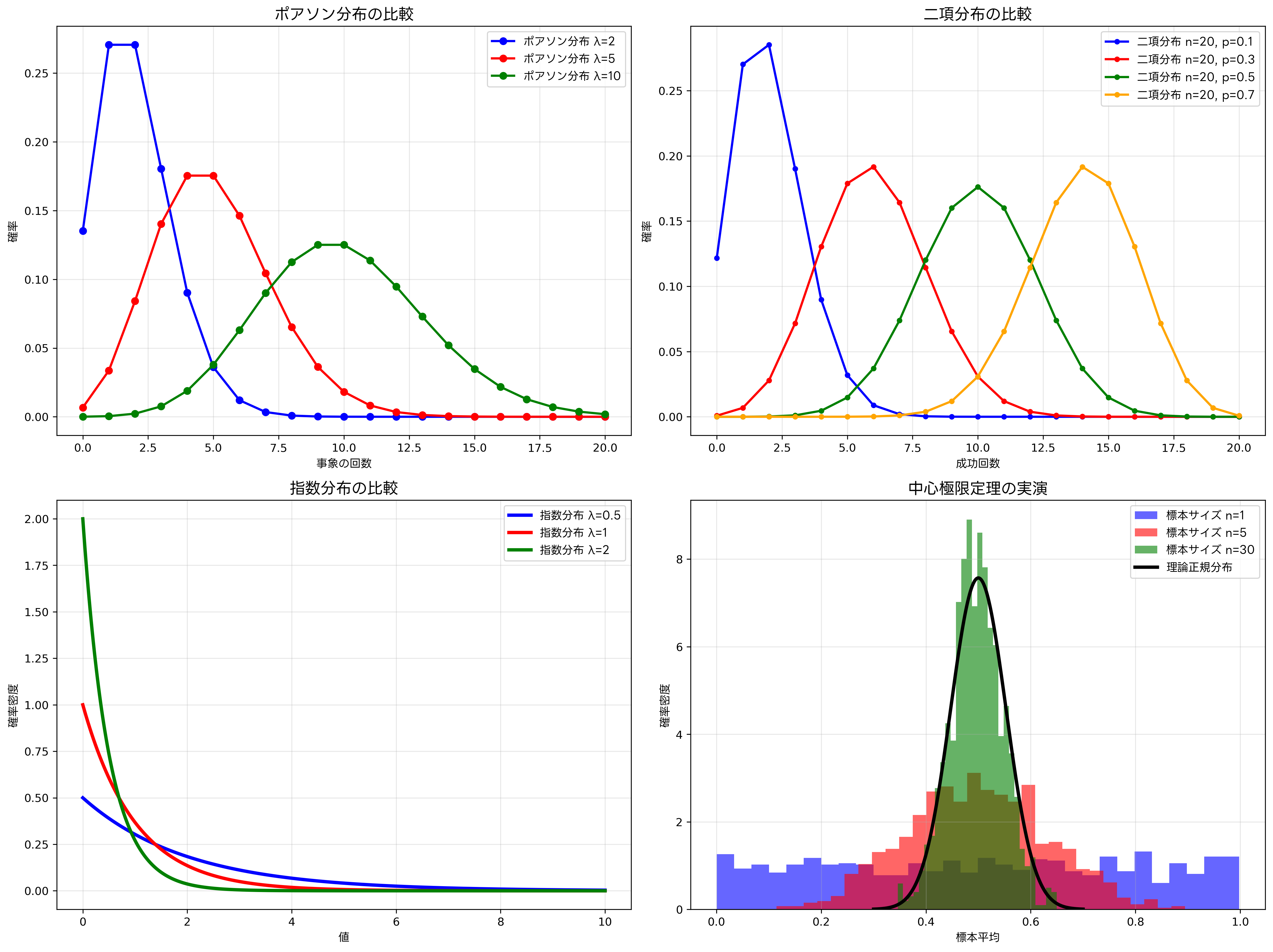
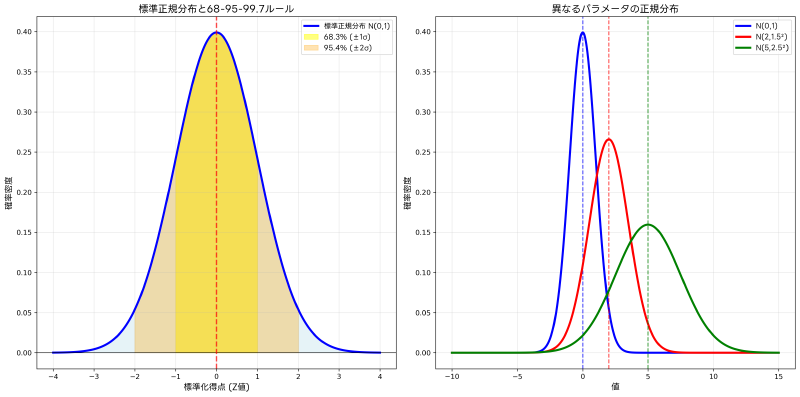
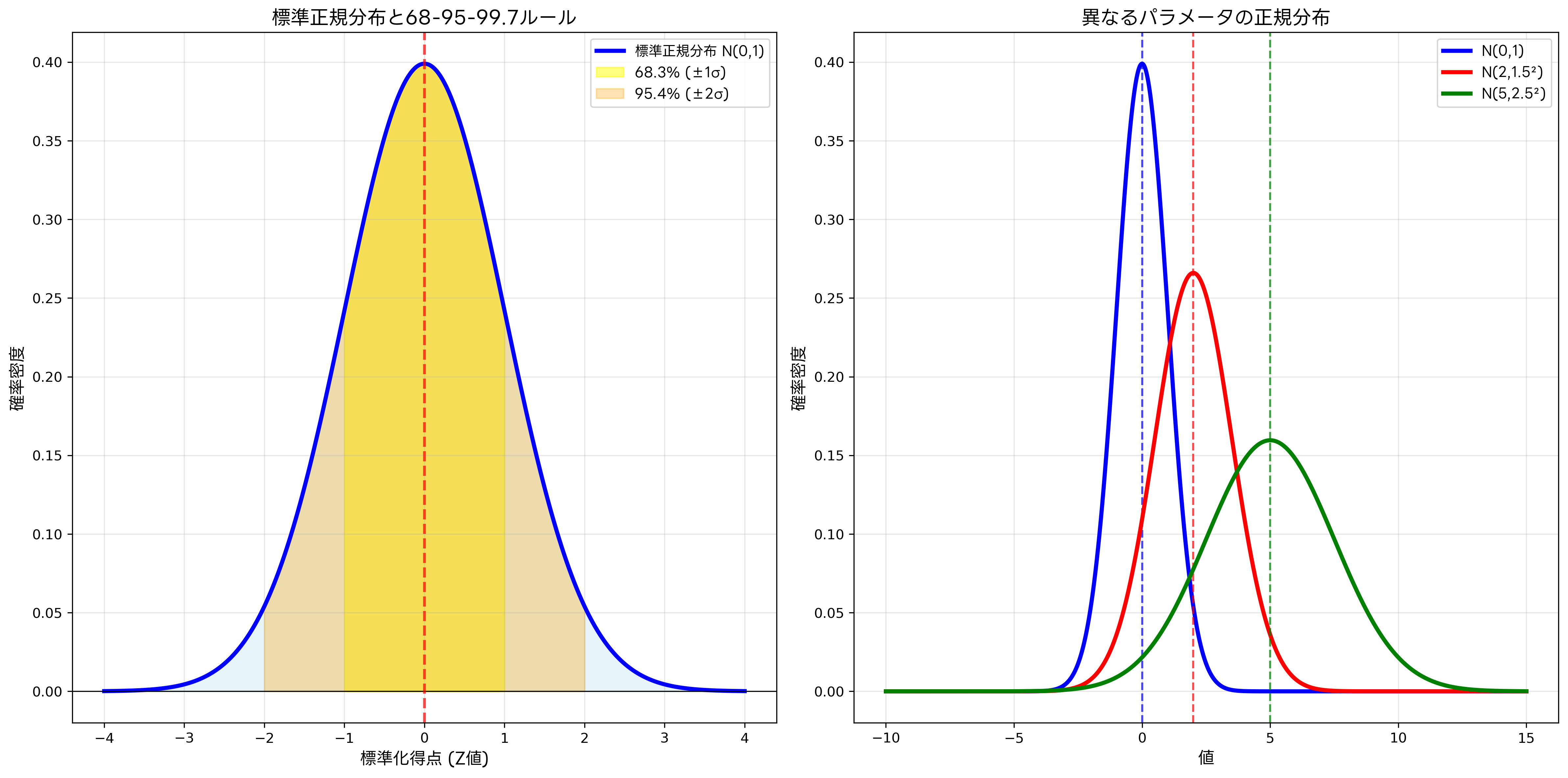
正規分布は統計学において最も重要な確率分布の一つです。中心極限定理により、多くの現実のデータが正規分布に近似できることが知られており、統計的推論の基礎となっています。正規分布の特徴的な性質である68-95-99.7ルール(経験則)は、品質管理や統計的品質検査装置の設計において広く活用されています。
ベイズの定理は、新たな情報を得た時に確率をどのように更新するかを示す重要な概念です。機械学習やAIの分野では、ベイズ統計解析ツールを使用してパラメータの事後分布を推定し、予測の不確実性を定量化する手法が注目されています。
確率論の応用範囲は広範囲にわたります。金融工学では、リスク管理システムにおいてVaR(Value at Risk)の計算に確率分布が使用され、潜在的な損失を定量的に評価しています。また、保険業界では、保険数理計算ソフトウェアを使用して事故や病気の発生確率をモデル化し、適切な保険料を設定しています。
推測統計学:標本から母集団を推論する
推測統計学は、限られた標本データから母集団全体の特徴を推測する統計学の分野です。この分野の中核となる概念には、点推定、区間推定(信頼区間)、仮説検定があります。これらの手法により、完全なデータを得ることが困難または不可能な状況でも、統計的に妥当な結論を導き出すことができます。
点推定は、標本統計量を用いて母集団パラメータの値を一つの数値で推定する方法です。標本平均は母平均の不偏推定量であり、標本分散は母分散の不偏推定量となります。推定量の良さを評価する基準には、不偏性、一致性、効率性があり、これらの性質を満たす推定量を選択することが重要です。
区間推定は、母集団パラメータが含まれる可能性の高い区間を求める方法です。信頼区間は、同じ方法で多数の標本を取った場合に、真の母集団パラメータを含む区間の割合を示します。95%信頼区間は、100回の標本抽出を行った場合に、約95回は真の値を含む区間が得られることを意味します。
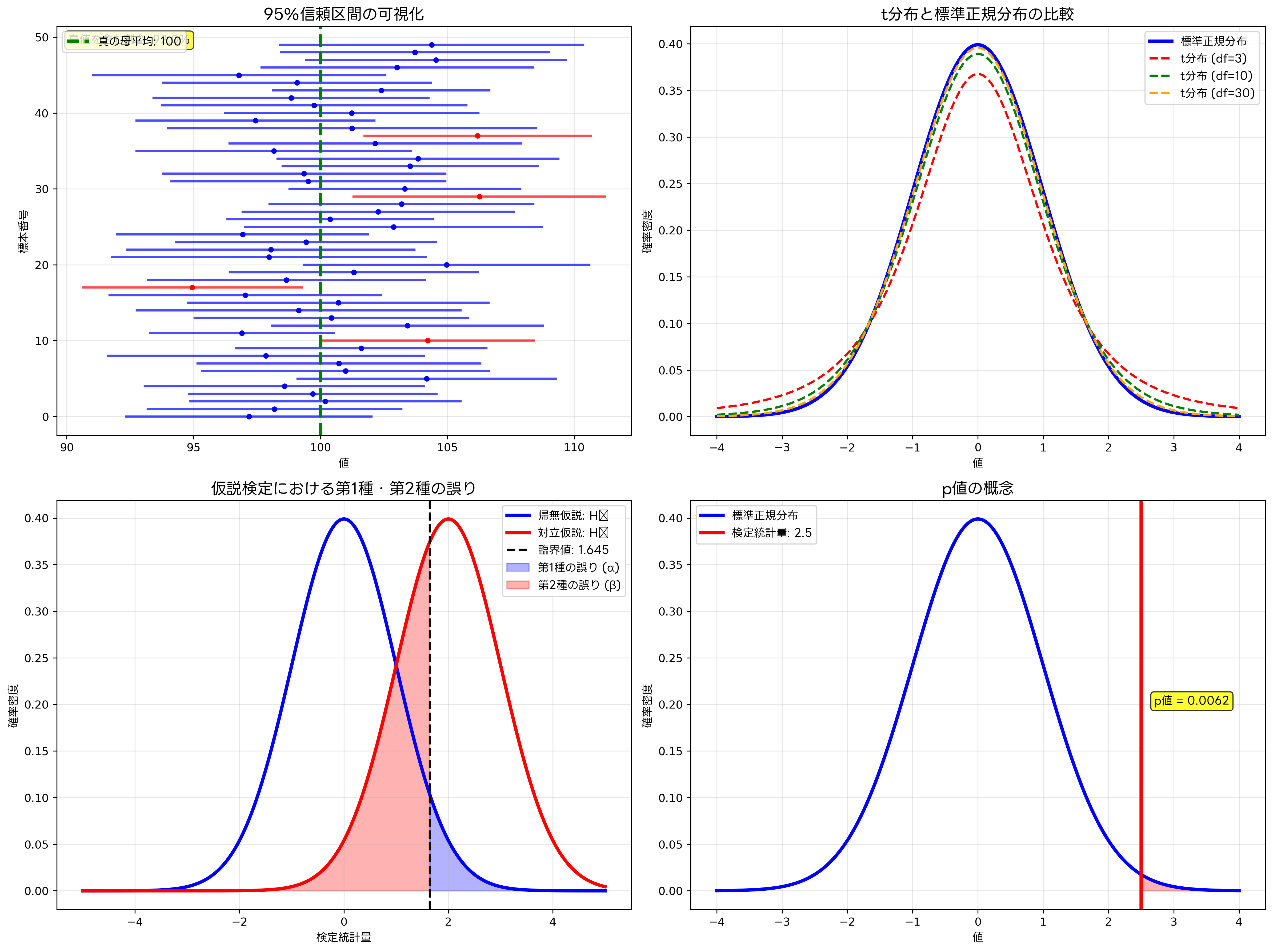
仮説検定は、母集団について立てた仮説の妥当性を統計的に検証する手法です。帰無仮説と対立仮説を設定し、標本データから計算した検定統計量と臨界値を比較することで、仮説の採択または棄却を決定します。この過程で発生する可能性のある誤りには、第1種の誤り(α誤り)と第2種の誤り(β誤り)があり、これらのバランスを考慮して検定を設計する必要があります。
t検定は最も基本的な仮説検定の一つで、母平均や二つの群の平均の差について検定を行います。実際の研究や業務では、統計検定ソフトウェアを使用することで、複雑な計算を自動化し、結果の解釈に集中できます。また、大規模なデータセットの分析には、高性能統計計算システムが必要になることもあります。
カイ二乗検定は、カテゴリカルデータの分析に使用される検定手法です。適合度検定では、データが特定の分布に従うかどうかを検定し、独立性検定では、二つのカテゴリカル変数が独立かどうかを検定します。マーケティングリサーチでは、アンケート分析システムを使用して、顧客の属性と購買行動の関連性を分析する際にカイ二乗検定が頻繁に使用されます。
回帰分析:変数間の関係をモデル化する
回帰分析は、一つまたは複数の説明変数を用いて目的変数を予測・説明するための統計手法です。単回帰分析では一つの説明変数を用い、重回帰分析では複数の説明変数を使用します。回帰分析により、変数間の関係を定量的に表現し、将来の値を予測することができます。
単回帰分析では、二つの変数間の線形関係を直線で表現します。回帰直線の傾きは説明変数が1単位変化したときの目的変数の変化量を表し、切片は説明変数が0のときの目的変数の値を表します。回帰分析の精度は決定係数(R²)で評価され、この値が1に近いほど説明変数が目的変数の変動をよく説明していることを意味します。
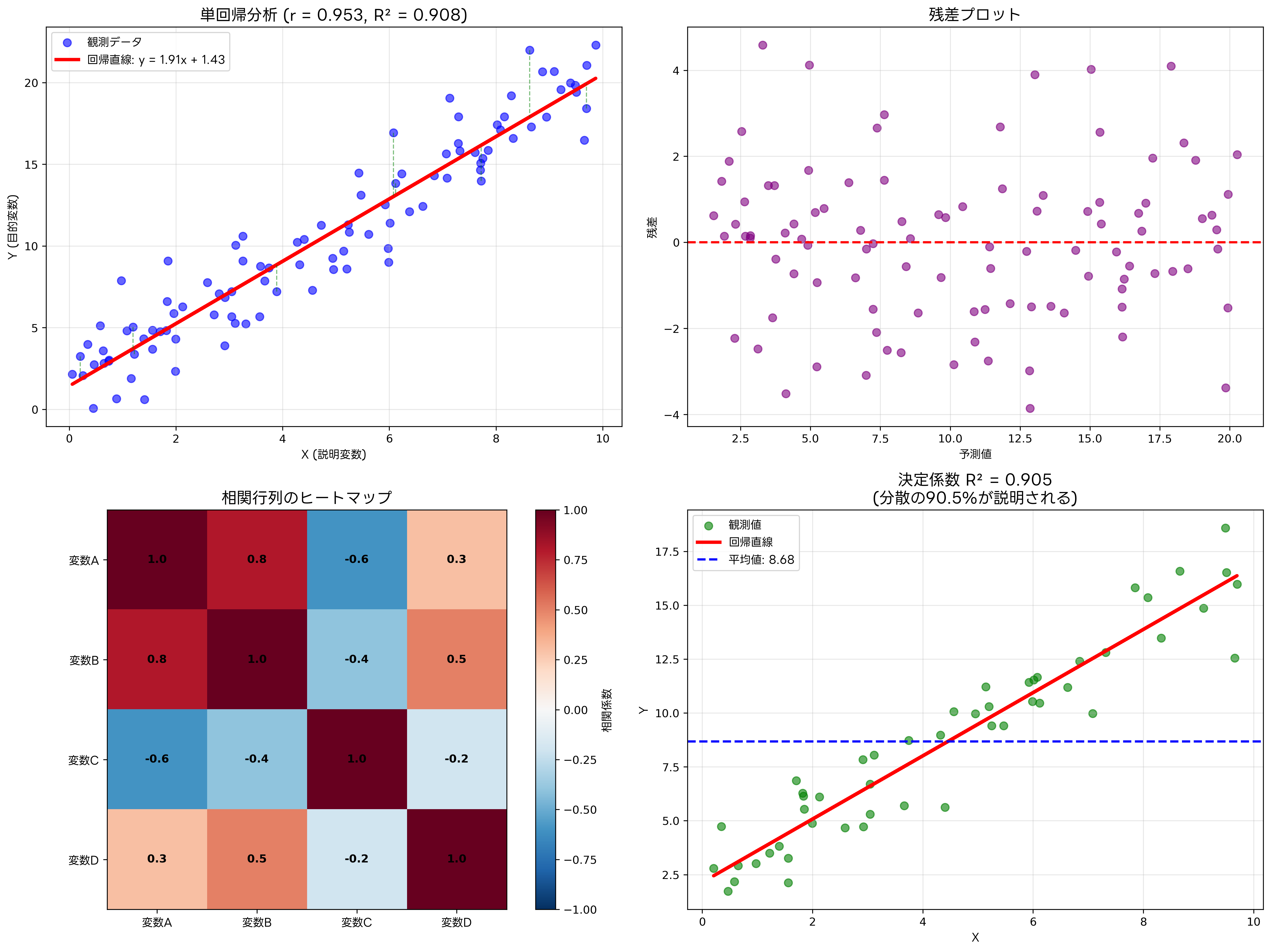
重回帰分析では、複数の説明変数を用いてより複雑な関係をモデル化できます。しかし、変数が増えることで多重共線性の問題が発生する可能性があります。多重共線性とは、説明変数同士に強い相関がある状況を指し、回帰係数の推定が不安定になる原因となります。この問題に対処するため、多重共線性診断ツールを使用して変数選択を適切に行う必要があります。
残差分析は回帰分析の妥当性を検証する重要な手法です。残差とは、観測値と予測値の差であり、理想的には残差は正規分布に従い、等分散性を満たすべきです。残差プロットを作成することで、モデルの前提条件が満たされているかどうかを視覚的に確認できます。
回帰分析の応用範囲は非常に広く、経済学、心理学、工学、医学など様々な分野で活用されています。売上予測では、売上予測システムにおいて過去の売上データ、広告費、季節要因などを説明変数として将来の売上を予測します。品質管理では、品質予測ツールを使用して製造条件から製品品質を予測し、不良品の発生を防ぐための対策を講じています。
分散分析:複数群の平均の差を検定する
分散分析(ANOVA)は、三つ以上の群の平均値に差があるかどうかを検定する統計手法です。t検定を複数回行うことで同様の結果を得ることもできますが、その場合は第1種の誤りの確率が累積的に増加してしまいます。分散分析を使用することで、この問題を回避しながら効率的に検定を行うことができます。
一元配置分散分析は、一つの要因について複数の水準(群)の効果を比較する手法です。例えば、三種類の教育方法の効果を比較する場合、各方法を受けた生徒の成績を比較して、方法間に有意な差があるかどうかを判定します。F統計量を用いて検定を行い、p値が有意水準を下回った場合は、少なくとも一つの群の平均が他と異なると結論できます。
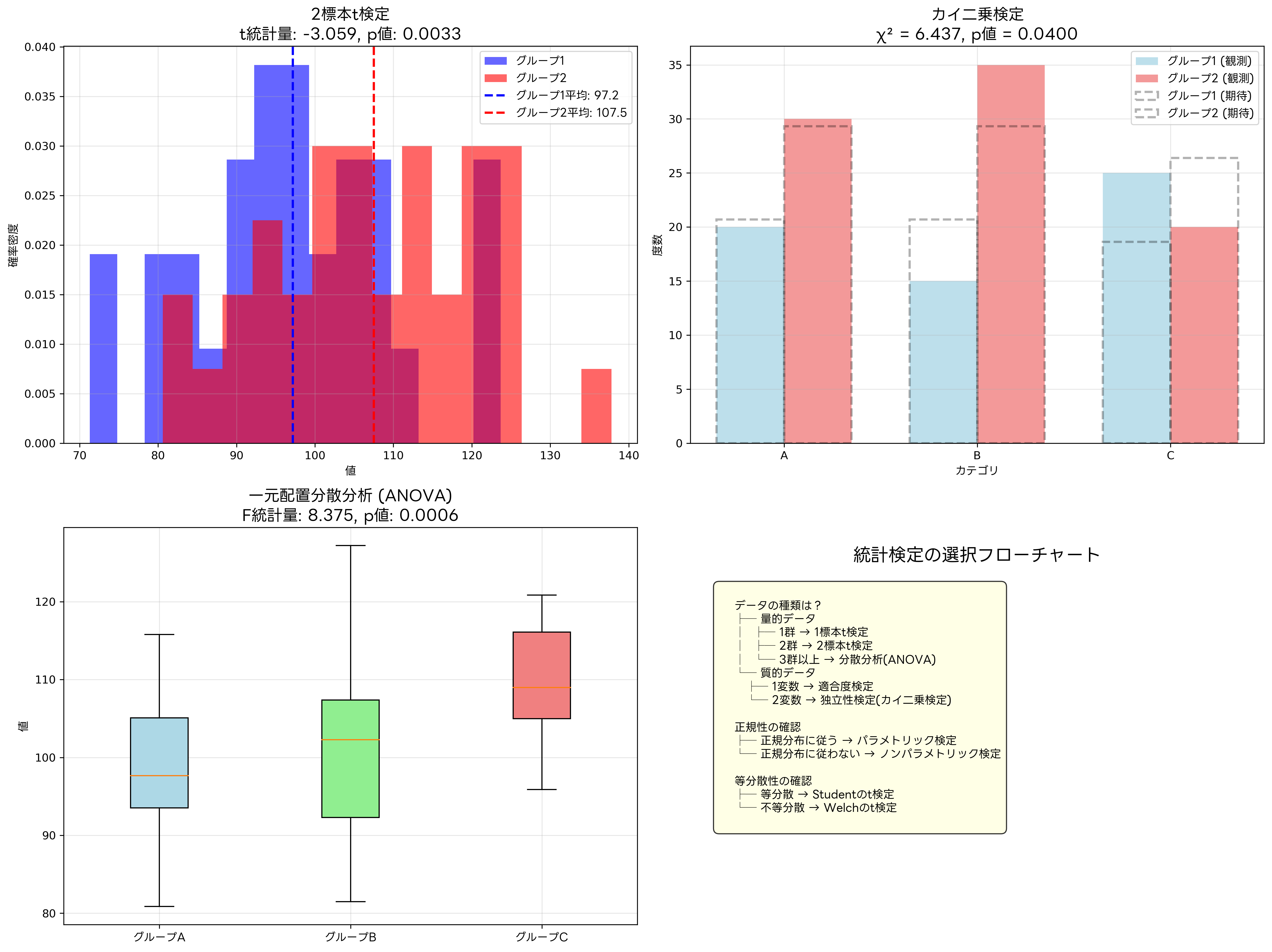
二元配置分散分析では、二つの要因とその交互作用効果を同時に検討できます。主効果は各要因が目的変数に与える効果であり、交互作用効果は二つの要因が組み合わさったときに生じる効果です。この手法により、より現実的で複雑な状況を統計的にモデル化することができます。
分散分析で有意差が検出された場合、どの群間に差があるのかを特定するために多重比較法を使用します。Tukeyの方法、Bonferroniの方法、Schefféの方法など、様々な多重比較法があり、それぞれ異なる特徴を持っています。統計的多重比較ソフトウェアを使用することで、これらの複雑な計算を効率的に実行できます。
分散分析は製造業の品質改善において特に重要な役割を果たしています。実験計画法ツールと組み合わせることで、製造条件の最適化や品質向上のための要因特定に活用されます。また、マーケティング分野では、A/Bテスト分析システムにおいて複数のマーケティング施策の効果比較に使用されています。
ノンパラメトリック検定:分布の仮定に依存しない手法
パラメトリック検定は、データが特定の分布(多くの場合は正規分布)に従うという仮定の下で実行されます。しかし、実際のデータがこの仮定を満たさない場合、検定結果の妥当性が問題となります。ノンパラメトリック検定は、分布の仮定に依存せず、データの順位や符号の情報を利用して検定を行う手法です。
Wilcoxonの符号付き順位検定は、対応のある二群のデータについて、中央値に差があるかどうかを検定する手法です。正規性の仮定が満たされない場合の対応のあるt検定の代替として使用されます。また、Mann-WhitneyのU検定は、対応のない二群のデータについて、分布の位置に差があるかどうかを検定します。
Kruskal-Wallis検定は、三つ以上の独立した群について、分布の位置に差があるかどうかを検定するノンパラメトリック手法です。一元配置分散分析の代替として使用され、データが正規分布に従わない場合や等分散性が満たされない場合に有効です。これらの手法は、ノンパラメトリック統計ソフトウェアを使用することで効率的に実行できます。
Spearmanの順位相関係数は、二つの変数間の単調な関係の強さを測定する指標です。Pearsonの積率相関係数とは異なり、変数間の線形関係だけでなく、非線形の単調関係も検出できます。この特性により、データマイニングツールにおいて、複雑な関係性を持つデータの分析に活用されています。
時系列分析:時間の要素を考慮したデータ分析
時系列データは、時間の経過とともに観測されるデータであり、経済データ、気象データ、株価データなどが典型的な例です。時系列分析では、データの中に含まれるトレンド、季節変動、循環変動、不規則変動の成分を分離し、将来の値を予測することを目的とします。
移動平均法は最も基本的な時系列分析手法の一つです。過去の一定期間のデータの平均値を計算することで、データの短期的な変動を平滑化し、長期的な傾向を把握できます。単純移動平均、加重移動平均、指数平滑法など、様々な移動平均法があり、データの特性に応じて適切な手法を選択する必要があります。
季節調整は、時系列データから季節変動成分を除去する手法です。経済統計では、季節調整ソフトウェアを使用してX-13ARIMA-SEATSやTRAMO-SEATSなどの高度な手法により、季節調整を行います。これにより、真の経済動向を正確に把握することができます。
ARIMA(自己回帰統合移動平均)モデルは、時系列分析における最も重要なモデルの一つです。自己回帰項、差分項、移動平均項を組み合わせることで、様々な時系列データの特性を表現できます。Box-Jenkins法による系統的なモデル選択手順により、適切なARIMAモデルを構築することができます。
時系列分析の応用分野は多岐にわたります。金融業界では、時系列分析システムを使用して株価や為替レートの予測を行い、投資判断の支援に活用しています。小売業では、需要予測ソフトウェアにより商品の売上予測を行い、在庫管理や調達計画の最適化を図っています。
応用情報技術者試験での統計学
応用情報技術者試験において、統計学は主にシステム開発における品質管理、性能評価、データ分析の文脈で出題されます。特に、品質管理における統計的手法、実験計画法、信頼性工学などの分野で統計学の知識が必要とされます。
午前問題では、統計学の基本概念、確率分布、仮説検定、回帰分析などの理論的知識が問われます。例えば、正規分布の特性、信頼区間の計算、回帰分析における決定係数の解釈などが出題されます。また、品質管理における管理図の読み方や、統計的工程管理の考え方についても理解が必要です。
午後問題では、より実践的な統計学の応用が問われます。システム開発プロジェクトにおける品質データの分析、性能テストデータの統計的評価、顧客満足度調査の分析手法などが出題範囲に含まれます。これらの問題を解くためには、統計学の理論を実際のビジネス場面に適用する能力が求められます。
試験対策としては、応用情報技術者試験統計問題集を使用して頻出問題のパターンを理解することが重要です。また、統計学基礎テキストにより理論的な理解を深め、実際の計算問題に慣れることが必要です。
統計学の現代的応用:ビッグデータとAI時代の統計学
現代の情報社会において、統計学の重要性はますます高まっています。ビッグデータの時代では、従来の統計手法だけでなく、機械学習や人工知能の技術と統計学が融合した新しい分析手法が注目されています。
機械学習における統計学の役割は非常に重要です。教師あり学習では回帰分析や分類問題として統計学の概念が応用され、教師なし学習ではクラスター分析や主成分分析などの多変量解析手法が基盤となっています。機械学習統計ツールを使用することで、これらの高度な分析を効率的に実行できます。
ベイズ統計学は、AI分野において特に注目されている統計手法です。事前分布と事後分布の概念により、新しい情報を得るたびに確率を更新し、より正確な予測を行うことができます。ベイズ機械学習システムは、不確実性を定量化した予測を提供し、意思決定の質を向上させます。
統計的品質管理では、Six Sigmaやリーン生産方式において統計学が中核的な役割を果たしています。Six Sigma統計ツールを使用することで、製造プロセスの変動を統計的に管理し、品質向上と コスト削減を同時に実現できます。
データサイエンスの分野では、統計学、計算機科学、専門分野の知識を融合した学際的アプローチが重要です。データサイエンス統合プラットフォームにより、データの収集から分析、可視化、レポート作成まで一連のプロセスを効率化できます。
まとめ:統計学の重要性と今後の展望
統計学は、不確実性に満ちた現実世界において、データに基づいた客観的な判断を可能にする強力なツールです。記述統計学によりデータの特徴を理解し、推測統計学により限られた情報から全体を推論し、実験計画法により効率的にデータを収集する。これらの手法を適切に活用することで、ビジネス、研究、政策立案などの様々な場面で価値ある洞察を得ることができます。
応用情報技術者試験の観点では、統計学は情報システムの品質保証や性能評価において不可欠な知識です。システムの信頼性を統計的に評価し、品質管理手法を適用し、データ分析により業務改善を図る能力は、現代のITプロフェッショナルに必須のスキルと言えるでしょう。
技術の進歩とともに、統計学の応用範囲は拡大し続けています。IoTデバイスから収集される大量のセンサーデータ、SNSから得られるソーシャルデータ、オンラインサービスの利用ログなど、新しい種類のデータが日々生成されています。これらのデータから価値を抽出するためには、従来の統計手法に加えて、機械学習や深層学習などの新しい技術との融合が必要です。
今後の統計学は、自動化と解釈可能性の両立が重要な課題となるでしょう。自動統計分析システムにより分析の効率化を図りながらも、結果の解釈と意思決定への活用においては人間の専門知識が不可欠です。統計学の理論的基礎を理解し、実践的な応用能力を身につけることで、データ駆動型社会における競争優位を確立できるでしょう。